mathbabe

This week in Rachel Schutt’s Columbia Data Science course we had two excellent guest speakers.

The first speaker of the night was Mark Hansen, who recently came from UCLA via the New York Times to Columbia with a joint appointment in journalism and statistics. He is a renowned data visualization expert and also an energetic and generous speaker. We were lucky to have him on a night where he’d been drinking an XXL latte from Starbucks to highlight his natural effervescence.

Mark started by telling us a bit about Gabriel Tarde (1843-1904).

Tarde was a sociologist who believed that the social sciences had the capacity to produce vastly more data than the physical sciences. His reasoning was as follows.

The physical sciences observe from a distance: they typically model or incorporate models which talk about an aggregate in some way – for example, biology talks about the aggregate of our cells. What Tarde pointed out was that this is a deficiency, basically a lack of information. We should instead be tracking every atom.

This is where Tarde points out that in the social realm we can do this, where cells are replaced by people. We can collect a huge amount of information about those individuals.

But wait, are we not missing the forest for the trees when we do this? Bruno Latour weighs in on his take of Tarde as follows:

“But the ‘whole’ is now nothing more than a provisional visualization which can be modified and reversed at will, by moving back to the individual components, and then looking for yet other tools to regroup the same elements into alternative assemblages.”

In 1903, Tarde even foresees the emergence of Facebook, although he refers to a “daily press”:

“At some point, every social event is going to be reported or observed.”

Mark then laid down the theme of his lecture using a 2009 quote of Bruno Latour:

“Change the instruments and you will change the entire social theory that goes with them.”

Kind of like that famous physics cat, I guess, Mark (and Tarde) want us to newly consider

1. the way the structure of society changes as we observe it, and
2. ways of thinking about the relationship of the individual to the aggregate.

Mark’s Thought Experiment:

As data become more personal, as we collect more data about “individuals”, what new methods or tools do we need to express the fundamental relationship between ourselves and our communities, our communities and our country, our country and the world? Could we ever be satisfied with poll results or presidential approval ratings when we can see the complete trajectory of public opinions, individuated and interacting?

What is data science?

Mark threw up this quote from our own John Tukey:

“The best thing about being a statistician is that you get to play in everyone’s backyard”

But let’s think about that again – is it so great? Is it even reasonable? In some sense, to think of us as playing in other people’s yards, with their toys, is to draw a line between “traditional data fields” and “everything else”.

It’s maybe even implying that all our magic comes from the traditional data fields (math, stats, CS), and we’re some kind of super humans because we’re uber-nerds. That’s a convenient way to look at it from the perspective of our egos, of course, but it’s perhaps too narrow and arrogant.

And it begs the question, what is “traditional” and what is “everything else” anyway?

Mark claims that everything else should include:

• social science,
• physical science,
• geography,
• architecture,
• education,
• information science,
• architecture,
• digital humanities,
• journalism,
• design,
• media art

There’s more to our practice than being technologists, and we need to realize that technology itself emerges out of the natural needs of a discipline. For example, GIS emerges from geographers and text data mining emerges from digital humanities.

In other words, it’s not math people ruling the world, it’s domain practices being informed by techniques growing organically from those fields. When data hits their practice, each practice is learning differently; their concerns are unique to that practice.

Responsible data science integrates those lessons, and it’s not a purely mathematical integration. It could be a way of describing events, for example. Specifically, it’s not necessarily a quantifiable thing.

Bottom-line: it’s possible that the language of data science has something to do with social science just as it has something to do with math.

Processing

Mark then told us a bit about his profile (“expansionist”) and about the language processing, in answer to a question about what is different when a designer takes up data or starts to code.

He explained it by way of another thought experiment: what is the use case for a language for artists? Students came up with a bunch of ideas:

• being able to specify shapes,
• faithful rendering of what visual thing you had in mind,
• being able to sketch,
• 3-d,
• animation,
• interactivity,
• Mark added publishing – artists must be able to share and publish their end results.

It’s java based, with a simple “publish” button, etc. The language is adapted to the practice of artists. He mentioned that teaching designers to code meant, for him, stepping back and talking about iteration, if statements, etc., of in other words stuff that seemed obvious to him but is not obvious to someone who is an artist. He needed to unpack his assumptions, which is what’s fun about teaching to the uninitiated.

He next moved on to close versus distant reading of texts. He mentioned Franco Moretti from Stanford. This is for Franco:

Franco thinks about “distant reading”, which means trying to get a sense of what someone’s talking about without reading line by line. This leads to PCA-esque thinking, a kind of dimension reduction of novels.

In other words, another cool example of how data science should integrate the way the experts in various fields figure it out. We don’t just go into their backyards and play, maybe instead we go in and watch themplay and formalize and inform their process with our bells and whistles. In this way they can teach us new games, games that actually expand our fundamental conceptions of data and the approaches we need to analyze them.

Mark’s favorite viz projects

1) Nuage Vert, Helen Evans & Heiko Hansen: a projection onto a power plant’s steam cloud. The size of the green projection corresponds to the amount of energy the city is using. Helsinki and Paris.

2) One Tree, Natalie Jeremijenko: The artist cloned trees and planted the genetically identical seeds in several areas. Displays among other things the environmental conditions in each area where they are planted.

3) Dusty Relief, New Territories: here the building collects pollution around it, displayed as dust.

4) Project Reveal, New York Times R&D lab: this is a kind of magic mirror which wirelessly connects using facial recognition technology and gives you information about yourself. As you stand at the mirror in the morning you get that “come-to-jesus moment” according to Mark.

5) Million Dollar Blocks, Spatial Information Design Lab (SIDL): So there are crime stats for google maps, which are typically painful to look at. The SIDL is headed by Laura Kurgan, and in this piece she flipped the statistics. She went into the prison population data, and for every incarcerated person, she looked at their home address, measuring per home how much money the state was spending to keep the people who lived there in prison. She discovered that some blocks were spending $1,000,000 to keep people in prison.

Moral of the above: just because you can put something on the map, doesn’t mean you should. Doesn’t mean there’s a new story. Sometimes you need to dig deeper and flip it over to get a new story.

New York Times lobby: Moveable Type

Mark walked us through a project he did with Ben Rubin for the NYTimes on commission (and he later went to the NYTimes on sabbatical). It’s in the lobby of their midtown headquarters at 8th and 42nd.

It consists of 560 text displays, two walls with 280 on each, and the idea is they cycle through various “scenes” which each have a theme and an underlying data science model.

For example, in one there are waves upon waves of digital ticker-tape like scenes which leave behind clusters of text, and where each cluster represents a different story from the paper. The text for a given story highlights phrases which make a given story different from others in some information-theory sense.

In another scene the numbers coming out of stories are highlighted, so you might see on a given box “18 gorillas”. In a third scene, crossword puzzles play themselves with sounds of pencil and paper.

The display boxes themselves are retro, with embedded linux processors running python, and a sound card on each box, which makes clicky sounds or wavy sounds or typing sounds depending on what scene is playing.

The data taken in is text from NY Times articles, blogs, and search engine activity. Every sentence is parsed using Stanford NLP techniques, which diagrams sentences.

Altogether there are about 15 “scenes” so far, and it’s code so one can keep adding to it. Here’s an interview with them about the exhibit:

Project Cascade: Lives on a Screen

Mark next told us about Cascade, which was joint work with Jer Thorp data artist-in-residence at the New York Times. Cascade came about from thinking about how people share New York Times links on Twitter. It was in partnerships with bitly.

The idea was to collect enough data so that we could see someone browse, encode the link in bitly, tweet that encoded link, see other people click on that tweet and see bitly decode the link, and then see those new people browse the New York Times. It’s a visualization of that entire process, much as Tarde suggested we should do.

There were of course data decisions to be made: a loose matching of tweets and clicks through time, for example. If 17 different tweets have the same url they don’t know which one you clicked on, so they guess (the guess actually seemed to involve probabilistic matching on time stamps so it’s an educated guess). They used the Twitter map of who follows who. If someone you follow tweets about something before you do then it counts as a retweet. It covers any nytimes.com link.

Here’s a NYTimes R&D video about Project Cascade:

Note: this was done 2 years ago, and Twitter has gotten a lot bigger since then.

Cronkite Plaza

Next Mark told us about something he was working on which just opened 1.5 months ago with Jer and Ben. It’s also news related, but this is projecting on the outside of a building rather than in the lobby; specifically, the communications building at UT Austin, in Cronkite Plaza.

The majority of the projected text is sourced from Cronkite’s broadcasts, but also have local closed-captioned news sources. One scene of this project has extracted the questions asked during local news – things like “how did she react?” or “What type of dog would you get?”. The project uses 6 projectors.

Goals of these exhibits

They are meant to be graceful and artistic, but should also teach something. At the same time we don’t want to be overly didactic. The aim is to live in between art and information. It’s a funny place: increasingly we see a flattening effect when tools are digitized and made available, so that statisticians can code like a designer (we can make things that look like design) and similarly designers can make something that looks like data.

What data can we get? Be a good investigator: a small polite voice which asks for data usually gets it.

eBay transactions and books

Again working jointly with Jer Thorp, Mark investigated a day’s worth of eBay’s transactions that went through Paypal and, for whatever reason, two years of book sales. How do you visualize this? Take a look at the yummy underlying data:

Here’s how they did it (it’s ingenious). They started with the text of Death of a Salesman by Arthur Miller. They used a mechanical turk mechanism to locate objects in the text that you can buy on eBay.

When an object is found it moves it to a special bin, so “chair” or “flute” or “table.” When it has a few collected buy-able objects, it then takes the objects and sees where they are all for sale on the day’s worth of transactions, and looks at details on outliers and such. After examining the sales, the code will find a zipcode in some quiet place like Montana.

Then it flips over to the book sales data, looks at all the books bought or sold in that zip code, picks a book (which is also on Project Gutenberg), and begins to read that book and collect “buyable” objects from that. And it keeps going. Here’s a video:

Public Theater Shakespeare Machine

The last thing Mark showed us is is joint work with Rubin and Thorp, installed in the lobby of the Public Theater. The piece itself is an oval structure with 37 bladed LED displays, set above the bar.

There’s one blade for each of Shakespeare’s plays. Longer plays are in the long end of the oval, Hamlet you see when you come in.

The data input is the text of each play. Each scene does something different – for example, it might collect noun phrases that have something to do with body from each play, so the “Hamlet” blade will only show a body phrase from Hamlet. In another scene, various kinds of combinations or linguistic constructs are mined:

• “high and might” “good and gracious” etc.
• “devilish-holy” “heart-sore” “ill-favored” “sea-tossed” “light-winged” “crest-fallen” “hard-favoured” etc.

Note here that the digital humanities, through the MONK Project, offered intense xml descriptions of the plays. Every single word is given hooha and there’s something on the order of 150 different parts of speech.

As Mark said, it’s Shakespeare so it stays awesome no matter what you do, but here we see we’re successively considering words as symbols, or as thematic, or as parts of speech. It’s all data.

Ian Wong from Square

Next Ian Wong, an “Inference Scientist” at Square who dropped out of an Electrical Engineering Ph.D. program at Stanford talked to us about Data Science in Risk.

He conveniently started with his takeaways:

1. Machine learning is not equivalent to R scripts. ML is founded in math, expressed in code, and assembled into software. You need to be an engineer and learn to write readable, reusable code: your code will be reread more times by other people than by you, so learn to write it so that others can read it.
2. Data visualization is not equivalent to producing a nice plot. Rather, think about visualizations as pervasive and part of the environment of a good company.
3. Together, they augment human intelligence. We have limited cognitive abilities as human beings, but if we can learn from data, we create an exoskeleton, an augmented understanding of our world through data.

Square

Square was founded in 2009. There were 40 employees in 2010, and there are 400 now. The mission of the company is to make commerce easy. Right now transactions are needlessly complicated. It takes too much to understand and to do, even to know where to start for a vendor. For that matter, it’s too complicated for buyers as well. The question we set out to ask is, how do we make transactions simple and easy?

We send out a white piece of plastic, which we refer to as the iconic square. It’s something you can plug into your phone or iPad. It’s simple and familiar, and it makes it easy to use and to sell.

It’s even possible to buy things hands-free using the square. A buyer can open a tab on their phone so that they can pay by saying their name.. Then the merchant taps your name on their screen. This makes sense if you are a frequent visitor to a certain store like a coffee shop.

Our goal is to make it easy for sellers to sign up for Square and accept payments. Of course, it’s also possible that somebody may sign up and try to abuse the service. We are therefore very careful at Square to avoid losing money on sellers with fraudulent intentions or bad business models.

The Risk Challenge

At Square we need to balance the following goals:

1. to provide a frictionless and delightful experience for buyers and sellers,
2. to fuel rapid growth, and in particular to avoid inhibiting growth through asking for too much information of new sellers, which adds needless barriers to joining, and
3. to maintain low financial loss.

Today we’ll just focus on the third goal through detection of suspicious activity. We do this by investing in machine learning and viz. We’ll first discuss the machine learning aspects.

Part 1: Detecting suspicious activity using machine learning

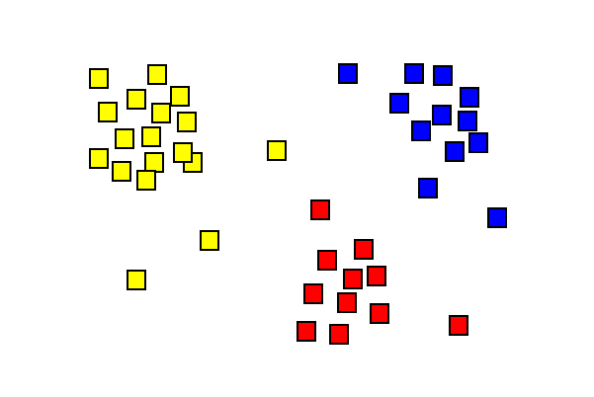
First of all, what’s suspicious? Examples from the class included:

1. lots of micro transactions occurring,
2. signs of money laundering,
3. high frequency or inconsistent frequency of transactions.

Example: Say Rachel has a food truck, but then for whatever reason starts to have $1000 transactions (mathbabe can’t help but insert that Rachel might be a food douche which would explain everything).

On the one hand, if we let money go through, Square is liable in the case it was unauthorized. Technically the fraudster, so in this case Rachel would be liable, but our experience is that usually fraudsters are insolvent, so it ends up on Square.

On the other hand, the customer service is bad if we stop payment on what turn out to be real payments. After all, what if she’s innocent and we deny the charges? She will probably hate us, may even sully our reputation, and in any case our trust is lost with her after that.

This example crystallizes the important challenges we face: false positives erode customer trust, false negatives make us lose money.

And since Square processes millions of dollars worth of sales per day, we need to do this systematically and automatically. We need to assess the risk level of every event and entity in our system.

So what do we do?

First of all, we take a look at our data. We’ve got three types:

1. payment data, where the fields are transaction_id, seller_id, buyer_id, amount, success (0 or 1), timestamp,
2. seller data, where the fields are seller_id, sign_up_date, business_name, business_type, business_location,
3. settlement data, where the fields are settlement_id, state, timestamp.

Important fact: we settle to our customers the next day so we don’t have to make our decision within microseconds. We have a few hours. We’d like to do it quickly of course, but in certain cases we have time for a phone call to check on things.

So here’s the process: given a bunch (as in hundreds or thousands) of payment events, we throw each through the risk engine, and then send some iffy looking ones on to a “manual review”. An ops team will then review the cases on an individual basis. Specifically, anything that looks rejectable gets sent to ops, which make phone calls to double check unless it’s super outrageously obviously fraud.

Also, to be clear, there are actually two kinds of fraud to worry about, seller-side fraud and buyer-side fraud. For the purpose of this discussion, we’ll focus on the former.

So now it’s a question of how we set up the risk engine. Note that we can think of the risk engine as putting things in bins, and those bins each have labels. So we can call this a labeling problem.

But that kind of makes it sound like unsupervised learning, like a clustering problem, and although it shares some properties with that, it’s certainly not that simple – we don’t reject a payment and then merely stand pat with that label, because as we discussed we send it on to an ops team to assess it independently. So in actuality we have a pretty complicated set of labels, including for example:

• initially rejected but ok,
• initially rejected and bad,
• initially accepted but on further consideration might have been bad,
• initially accepted and things seem ok,
• initially accepted and later found to be bad, …

So in other words we have ourselves a semi-supervised learning problem, straddling the worlds of supervised and unsupervised learning. We first check our old labels, and modify them, and then use them to help cluster new events using salient properties and attributes common to historical events whose labels we trust. We are constantly modifying our labels even in retrospect for this reason.

We estimate performance  using precision and recall. Note there are very few positive examples so accuracy is not a good metric of success, since the “everything looks good” model is dumb but has good accuracy.

Labels are what Ian considered to be the “neglected half of the data” (recall T = {(x_i, y_i)}). In undergrad statistics education and in data mining competitions, the availability of labels is often taken for granted. In reality, labels are tough to define and capture. Labels are really important. It’s not just objective function, it is the objective.

As is probably familiar to people, we have a problem with sparsity of features. This is exacerbated by class imbalance (i.e., there are few positive samples). We also don’t know the same information for all of our sellers, especially when we have new sellers. But if we are too conservative we start off on the wrong foot with new customers.

Also, we might have a data point, say zipcode, for every seller, but we don’t have enough information in knowing the zipcode alone because so few sellers share zipcodes. In this case we want to do some clever binning of the zipcodes, which is something like sub model of our model.

Finally, and this is typical for predictive algorithms, we need to tweak our algorithm to optimize it- we need to consider whether features interact linearly or non-linearly, and to account for class imbalance.. We also have to be aware of adversarial behavior. An example of adversarial behavior in e-commerce is new buyer fraud, where a given person sets up 10 new accounts with slightly different spellings of their name and address.

Since models degrade over time, as people learn to game them, we need to continually retrain models. The keys to building performance models are as follows:

• it’s not a black box. You can’t build a good model by assuming that the algorithm will take care of everything. For instance, I need to know why I am misclassifying certain people, so I’ll need to roll up my sleeves and dig into my model.
• We need to perform rapid iterations of testing, with experiments like you’d do in a science lab. If you’re not sure whether to try A or B, then try both.
• When you hear someone say, “So which models or packages do you use?” then you’ve got someone who doesn’t get it. Models and/or packages are not magic potion.

Mathbabe cannot resist paraphrasing Ian here as saying “It’s not about the package. it’s about what you do with it.” But what Ian really thinks it’s about, at least for code, is:

• readability
• reusability
• correctness
• structure
• hygiene

So, if you’re coding a random forest algorithm and you’ve hardcoded the number of trees: you’re an idiot. put a friggin parameter there so people can reuse it. Make it tweakable. And write the tests for pity’s sake; clean code and clarity of thought go together.

At Square we try to maintain reusability and readability — we structure our code in different folders with distinct, reusable components that provide semantics around the different parts of building a machine learning model: model, signal, error, experiment.

We only write scripts in the experiments folder where we either tie together components from model, signal and error or we conduct exploratory data analysis. It’s more than just a script, it’s a way of thinking, a philosophy of approach.

What does such a discipline give you? Every time you run an experiment your should incrementally increase your knowledge. This discipline helps you make sure you don’t do the same work again. Without it you can’t even figure out the things you or someone else has already attempted.

For more on what every project directory should contain, see Project Template, written by John Myles White.

We had a brief discussion of how reading other people’s code is a huge problem, especially when we don’t even know what clean code looks like. Ian stayed firm on his claim that “if you don’t write production code then you’re not productive.”

In this light, Ian suggests exploring and actively reading Github’s repository of R code. He says to try writing your own R package after reading this. Also, he says that developing an aesthetic sense for code is analogous to acquiring the taste for beautiful proofs; it’s done through rigorous practice and feedback from peers and mentors. The problem is, he says, that statistics instructors in schools usually do not give feedback on code quality, nor are they qualified to.

For extra credit, Ian suggests the reader contrasts the implementations of the caret package (poor code) with scikit-learn (clean code).

Important things Ian skipped

• how is a model “productionized”?
• how are features computed in real-time to support these models?
• how do we make sure “what we see is what we get”, meaning the features we build in a training environment will be the ones we see in real-time. Turns out this is a pretty big problem.
• how do you test a risk engine?

Next Ian talked to us about how Square uses visualization.

Data Viz at Square

Ian talked to us about a bunch of different ways the Inference Team at Square use visualizations to monitor the transactions going on at any given time. He mentioned that these monitors aren’t necessarily trying to predict fraud per se but rather provides a way of keeping an eye on things to look for trends and patterns over time and serves as the kind of “data exoskeleton” that he mentioned at the beginning. People at Square believe in ambient analytics, which means passively ingesting data constantly so you develop a visceral feel for it.

After all, it is only by becoming very familiar with our data that we even know what kind of patterns are unusual or deserve their own model. To go further into the philosophy of this approach, he said two thing:

“What gets measured gets managed,” and “You can’t improve what you don’t measure.”

He described a workflow tool to review users, which shows features of the seller, including the history of sales and geographical information, reviews, contact info, and more. Think mission control.

In addition to the raw transactions, there are risk metrics that Ian keeps a close eye on. So for example he monitors the “clear rates” and “freeze rates” per day, as well as how many events needed to be reviewed. Using his fancy viz system he can get down to which analysts froze the most today and how long each account took to review, and what attributes indicate a long review process.

In general people at Square are big believers in visualizing business metrics (sign-ups, activations, active users, etc.) in dashboards; they think it leads to more accountability and better improvement of models as they degrade. They run a kind of constant EKG of their business through ambient analytics.

Ian ended with his data scientist profile. He thinks it should be on a logarithmic scale, since it doesn’t take very long to be okay at something (good enough to get by) but it takes lots of time to get from good to great. He believes that productivity should also be measured in log-scale, and his argument is that leading software contributors crank out packages at a much higher rate than other people.

Ian’s advice to aspiring data scientists

1. play with real data
2. build a good foundation in school
3. get an internship
4. be literate, not just in statistics
5. stay curious

Ian’s thought experiment

Suppose you know about every single transaction in the world as it occurs. How would you use that data?

This week our guest lecturer for the Columbia Data Science class was Brian Dalessandro. Brian works at Media6Degrees as a VP of Data Science, and he’s super active in the research community. He’s also served as co-chair of the KDD competition.

Before Brian started, Rachel threw us a couple of delicious data science tidbits.

The Process of Data Science

First we have the Real World. Inside the Real World we have:

• Users using Google+
• People competing in the Olympics
• Spammers sending email

From this we draw raw data, e.g. logs, all the olympics records, or Enron employee emails. We want to process this to make it clean for analysis. We use pipelines of data munging, joining, scraping, wrangling or whatever you want to call it and we use tools such as:

• python
• shell scripts
• R
• SQL

We eventually get the data down to a nice format, say something with columns:

name event year gender event time

Note: this is where you typically start in a standard statistics class. But it’s not where we typically start in the real world.

Once you have this clean data set, you should be doing some kind of exploratory data analysis (EDA); if you don’t really know what I’m talking about then look at Rachel’s recent blog post on the subject. You may realize that it isn’t actually clean.

Next, you decide to apply some algorithm you learned somewhere:

• k-nearest neighbor
• regression
• Naive Bayes
• (something else),

depending on the type of problem you’re trying to solve:

• classification
• prediction
• description

You then:

• interpret
• visualize
• report
• communicate

At the end you have a “data product”, e.g. a spam classifier.

K-means

So far we’ve only seen supervised learning. K-means is the first unsupervised learning technique we’ll look into. Say you have data at the user level:

• G+ data
• survey data
• medical data
• SAT scores

Assume each row of your data set corresponds to a person, say each row corresponds to information about the user as follows:

age gender income Geo=state household size

Your goal is to segment them, otherwise known as stratify, or group, or cluster. Why? For example:

• you might want to give different users different experiences. Marketing often does this.
• you might have a model that works better for specific groups
• hierarchical modeling in statistics does something like this.

One possibility is to choose the groups yourself. Bucket users using homemade thresholds. Like by age, 20-24, 25-30, etc. or by income. In fact, say you did this, by age, gender, state, income, marital status. You may have 10 age buckets, 2 gender buckets, and so on, which would result in 10x2x50x10x3 = 30,000 possible bins, which is big.

You can picture a five dimensional space with buckets along each axis, and each user would then live in one of those 30,000 five-dimensional cells. You wouldn’t want 30,000 marketing campaigns so you’d have to bin the bins somewhat.

Wait, what if you want to use an algorithm instead where you could decide on the number of bins? K-means is a “clustering algorithm”, and k is the number of groups. You pick k, a hyper parameter.

2-d version

Say you have users with #clicks, #impressions (or age and income – anything with just two numerical parameters). Then k-means looks for clusters on the 2-d plane. Here’s a stolen and simplistic picture that illustrates what this might look like:

The general algorithm is just the same picture but generalized to d dimensions, where d is the number of features for each data point.

Here’s the actual algorithm:

• randomly pick K centroids
• assign data to closest centroid.
• move the centroids to the average location of the users assigned to it
• repeat until the assignments don’t change

It’s up to you to interpret if there’s a natural way to describe these groups.

This is unsupervised learning and it has issues:

• choosing an optimal k is also a problem although , where n is number of data points.
• convergence issues – the solution can fail to exist (the configurations can fall into a loop) or “wrong”
• but it’s also fast
• interpretability can be a problem – sometimes the answer isn’t useful
• in spite of this, there are broad applications in marketing, computer vision (partition an image), or as a starting point for other models.

One common tool we use a lot in our systems is logistic regression.

Thought Experiment

Brian now asked us the following:

How would data science differ if we had a “grand unified theory of everything”?

He gave us some thoughts:

• Would we even need data science?
• Theory offers us a symbolic explanation of how the world works.
• What’s the difference between physics and data science?
• Is it just accuracy? After all, Newton wasn’t completely precise, but was pretty close.

If you think of the sciences as a continuum, where physics is all the way on the right, and as you go left, you get more chaotic, then where is economics on this spectrum? Marketing? Finance? As we go left, we’re adding randomness (and as a clever student points out, salary as well).

Bottomline: if we could model this data science stuff like we know how to model physics, we’d know when people will click on what ad. The real world isn’t this understood, nor do we expect to be able to in the future.

Does “data science” deserve the word “science” in its name? Here’s why maybe the answer is yes.

We always have more than one model, and our models are always changing.

The art in data science is this: translating the problem into the language of data science

The science in data science is this: given raw data, constraints and a problem statement, you have an infinite set of models to choose from, with which you will use to maximize performance on some evaluation metric, that you will have to specify. Every design choice you make can be formulated as an hypothesis, upon which you will use rigorous testing and experimentation to either validate or refute.

Never underestimate the power of creativity: usually people have vision but no method. As the data scientist, you have to turn it into a model within the operational constraints. You need to optimize a metric that you get to define. Moreover, you do this with a scientific method, in the following sense.

Namely, you hold onto your existing best performer, and once you have a new idea to prototype, then you set up an experiment wherein the two best models compete. You therefore have a continuous scientific experiment, and in that sense you can justify it as a science.

Classifiers

Given

• data
• a problem, and
• constraints,

we need to determine:

• a classifier,
• an optimization method,
• a loss function,
• features, and
• an evaluation metric.

Today we will focus on the process of choosing a classifier.

Classification involves mapping your data points into a finite set of labels or the probability of a given label or labels. Examples of when you’d want to use classification:

• will someone click on this ad?
• what number is this?
• what is this news article about?
• is this spam?
• is this pill good for headaches?

From now on we’ll talk about binary classification only (0 or 1).

Examples of classification algorithms:

• decision tree
• random forests
• naive bayes
• k-nearest neighbors
• logistic regression
• support vector machines
• neural networks

Which one should we use?

One possibility is to try them all, and choose the best performer. This is fine if you have no constraints or if you ignore constraints. But usually constraints are a big deal – you might have tons of data or not much time or both.

If I need to update 500 models a day, I do need to care about runtime. these end up being bidding decisions. Some algorithms are slow – k-nearest neighbors for example. Linear models, by contrast, are very fast.

One under-appreciated constraint of a data scientist is this: your own understanding of the algorithm.

Ask yourself carefully, do you understand it for real? Really? Admit it if you don’t. You don’t have to be a master of every algorithm to be a good data scientist. The truth is, getting the “best-fit” of an algorithm often requires intimate knowledge of said algorithm. Sometimes you need to tweak an algorithm to make it fit your data. A common mistake for people not completely familiar with an algorithm is to overfit.

Another common constraint: interpretability. You often need to be able to interpret your model, for the sake of the business for example. Decision trees are very easy to interpret. Random forests, on the other hand, not so much, even though it’s almost the same thing, but can take exponentially longer to explain in full. If you don’t have 15 years to spend understanding a result, you may be willing to give up some accuracy in order to have it easy to understand.

Note that credit cards have to be able to explain their models by law so decision trees make more sense than random forests.

How about scalability? In general, there are three things you have to keep in mind when considering scalability:

• learning time: how much time does it take to train the model?
• scoring time: how much time does it take to give a new user a score once the model is in production?
• model storage: how much memory does the production model use up?

Here’s a useful paper to look at when comparing models: “An Empirical Comparison of Supervised Learning Algorithms”, from which we learn:

• Simpler models are more interpretable but aren’t as good performers.
• The question of which algorithm works best is problem dependent
• It’s also constraint dependent

At M6D, we need to match clients (advertising companies) to individual users. We have logged the sites they have visited on the internet. Different sites collect this information for us. We don’t look at the contents of the page – we take the url and hash it into some random string and then we have, say, the following data about a user we call “u”:

u = <xyz, 123, sdqwe, 13ms>

This means u visited 4 sites and their urls hashed to the above strings. Recall last week we learned spam classifier where the features are words. We aren’t looking at the meaning of the words. So the might as well be strings.

At the end of the day we build a giant matrix whose columns correspond to sites and whose rows correspond to users, and there’s a “1” if that user went to that site.

To make this a classifier, we also need to associate the behavior “clicked on a shoe ad”. So, a label.

Once we’ve labeled as above, this looks just like spam classification. We can now rely on well-established methods developed for spam classification – reduction to a previously solved problem.

Logistic Regression

We have three core problems as data scientists at M6D:

• feature engineering,
• user level conversion prediction,
• bidding.

We will focus on the second. We use logistic regression– it’s highly scalable and works great for binary outcomes.

What if you wanted to do something else? You could simply find a threshold so that, above you get 1, below you get 0. Or you could use a linear model like linear regression, but then you’d need to cut off below 0 or above 1.

What’s better: fit a function that is bounded in side [0,1]. For example, the logit function

wanna estimate

.

To make this a linear model in the outcomes , we take the log of the odds ratio:

The parameter keeps shape of the logit curve but shifts it back and forth. To interpret further, consider what we call the base rate, the unconditional probability of “1” (so, in the case of ads, the base rate would correspond to the click-through rate, i.e. the overall tendency for people to click on ads; this is typically on the order of 1%).

If you had no information except the base rate, the average prediction would be just that. In a logistical regression, defines the base rate. Specifically, the base rate is approximately equal to

The slope defines the slope of the logit function. Note in general it’s a vector which is as long as the number of features we are using for each data point.

Our immediate modeling goal is to use our training data to find the best choices for and We will use a maximum likelihood estimation or convex optimization to achieve this; we can’t just use derivatives and vector calculus like we did with linear regression because it’s a complicated function of our data.

The likelihood function is defined by:

where we are assuming the data points are independent and where

We then search for the parameters that maximize this having observed our data:

The probability of a single observation is

where is the modeled probability of a “1” for the binary outcome $Y_i.$ Taking the product of all of these we get our likelihood function which we want to maximize.

Similar to last week, we now take the log and get something convex, so it has to have a global maximum. Finally, we use numerical techniques to find it, which essentially follow the gradient like Newton’s method from calculus. Computer programs can do this pretty well. These algorithms depend on a step size, which we will need to adjust as we get closer to the global max or min – there’s an art to this piece of numerical optimization as well. Each step of the algorithm looks something like this:

where remember we are actually optimizing our parameters and to maximize the (log) likelihood function, so the you see above is really a vector of s and the function corresponds to our

“Flavors” of Logistic Regression for convex optimization.

The Newton’s method we described above is also called Iterative Reweighted Least Squares. It uses the curvature of log-likelihood to choose appropriate step direction. The actual calculation involves the Hessian matrix, and in particular requires its inversion, which is a kxk matrix. This is bad when there’s lots of features, as in 10,000 or something. Typically we don’t have that many features but it’s not impossible.

Another possible method to maximize our likelihood or log likelihood is called Stochastic Gradient Descent. It approximates gradient using a single observation at a time. The algorithm updates the current best-fit parameters each time it sees a new data point. The good news is that there’s no big matrix inversion, and it works well with huge data and with sparse features; it’s a big deal in Mahout and Vowpal Wabbit. The bad news is it’s not such a great optimizer and it’s very dependent on step size.

Evaluation

We generally use different evaluation metrics for different kind of models.

First, for ranking models, where we just want to know a relative rank versus and absolute score, we’d look to one of:

• area under the receiver operating curve (AUC)
• area under the cumulative lift curve

Second, for classification models, we’d look at the following metrics:

• lift: how much more people are buying or clicking because of a model
• accuracy: how often the correct outcome is being predicted
• f-score
• precision
• recall

Finally, for density estimation, where we need to know an actual probability rather than a relative score, we’d look to:

• mean absolute error
• mean squared error

In general it’s hard to compare lift curves but you can compare AUC (area under the receiver operator curve) – they are “base rate invariant.” In other words if you bring the click-through rate from 1% to 2%, that’s 100% lift but if you bring it from 4% to 7% that’s less lift but more effect. AUC does a better job in such a situation when you want to compare.

Density estimation tests tell you how well are you fitting for conditional probability. In advertising, this may arise if you have a situation where each ad impression costs $c and for each conversion you receive $q. You will want to target every conversion that has a positive expected value, i.e. whenever

But to do this you need to make sure the probability estimate on the left is accurate, which in this case means something like the mean squared error of the estimator is small. Note a model can give you good rankings but bad P estimates.

Similarly, features that rank highly on AUC don’t necessarily rank well with respect to mean absolute error. So feature selection, as well as your evaluation method, is completely context-driven.

In the third week of the Columbia Data Science course, our guest lecturer was Jake Hofman. Jake is at Microsoft Research after recently leaving Yahoo! Research. He got a Ph.D. in physics at Columbia and taught a fantastic course on modeling last semester at Columbia.

After introducing himself, Jake drew up his “data science profile;” turns out he is an expert on a category that he created called “data wrangling.” He confesses that he doesn’t know if he spends so much time on it because he’s good at it or because he’s bad at it.

Thought Experiment: Learning by Example

Jake had us look at a bunch of text. What is it? After some time we describe each row as the subject and first line of an email in Jake’s inbox. We notice the bottom half of the rows of text looks like spam.

Now Jake asks us, how did you figure this out? Can you write code to automate the spam filter that your brain is?

Some ideas the students came up with:

• Any email is spam if it contains Viagra references. Jake: this will work if they don’t modify the word.
• Maybe something about the length of the subject?
• Exclamation points may point to spam. Jake: can’t just do that since “Yahoo!” would count.
• Jake: keep in mind spammers are smart. As soon as you make a move, they game your model. It would be great if we could get them to solve important problems.
• Should we use a probabilistic model? Jake: yes, that’s where we’re going.
• Should we use k-nearest neighbors? Should we use regression? Recall we learned about these techniques last week. Jake: neither. We’ll use Naive Bayes, which is somehow between the two.

Why is linear regression not going to work?

Say you make a feature for each lower case word that you see in any email and then we used R’s “lm function:”

lm(spam ~ word1 + word2 + …)

Wait, that’s too many variables compared to observations! We have on the order of 10,000 emails with on the order of 100,000 words. This will definitely overfit. Technically, this corresponds to the fact that the matrix in the equation for linear regression is not invertible. Moreover, maybe can’t even store it because it’s so huge.

Maybe you could limit to top 10,000 words? Even so, that’s too many variables vs. observations to feel good about it.

Another thing to consider is that target is 0 or 1 (0 if not spam, 1 if spam), whereas you wouldn’t get a 0 or a 1 in actuality through using linear regression, you’d get a number. Of course you could choose a critical value so that above that we call it “1” and below we call it “0”. Next week we’ll do even better when we explore logistic regression, which is set up to model a binary response like this.

How about k-nearest neighbors?

To use k-nearest neighbors we would still need to choose features, probably corresponding to words, and you’d likely define the value of those features to be 0 or 1 depending on whether the word is present or not. This leads to a weird notion of “nearness”.

Again, with 10,000 emails and 100,000 words, we’ll encounter a problem: it’s not a singular matrix this time but rather that the space we’d be working in has too many dimensions. This means that, for example, it requires lots of computational work to even compute distances, but even that’s not the real problem.

The real problem is even more basic: even your nearest neighbors are really far away. this is called “the curse of dimensionality“. This problem makes for a poor algorithm.

Question: what if sharing a bunch of words doesn’t mean sentences are near each other in the sense of language? I can imagine two sentences with the same words but very different meanings.

Jake: it’s not as bad as it sounds like it might be – I’ll give you references at the end that partly explain why.

Aside: digit recognition

In this case k-nearest neighbors works well and moreover you can write it in a few lines of R.

Take your underlying representation apart pixel by pixel, say in a 16 x 16 grid of pixels, and measure how bright each pixel is. Unwrap the 16×16 grid and put it into a 256-dimensional space, which has a natural archimedean metric. Now apply the k-nearest neighbors algorithm.

Some notes:

• If you vary the number of neighbors, it changes the shape of the boundary and you can tune k to prevent overfitting.
• You can get 97% accuracy with a sufficiently large data set.
• Result can be viewed in a “confusion matrix“.

Naive Bayes

Question: You’re testing for a rare disease, with 1% of the population is infected. You have a highly sensitive and specific test:

• 99% of sick patients test positive
• 99% of healthy patients test negative

Given that a patient tests positive, what is the probability that the patient is actually sick?

Answer: Imagine you have 100×100 = 10,000 people. 100 are sick, 9,900 are healthy. 99 sick people test sick, and 99 healthy people do too. So if you test positive, you’re equally likely to be healthy or sick. So the answer is 50%.

Let’s do it again using fancy notation so we’ll feel smart:

Recall

and solve for

The denominator can be thought of as a “normalization constant;” we will often be able to avoid explicitly calculuating this. When we apply the above to our situation, we get:

This is called “Bayes’ Rule“. How do we use Bayes’ Rule to create a good spam filter? Think about it this way: if the word “Viagra” appears, this adds to the probability that the email is spam.

To see how this will work we will first focus on just one word at a time, which we generically call “word”. Then we have:

The right-hand side of the above is computable using enough pre-labeled data. If we refer to non-spam as “ham”, we only need and This is essentially a counting exercise.

Example: go online and download Enron emails. Awesome. We are building a spam filter on that – really this means we’re building a new spam filter on top of the spam filter that existed for the employees of Enron.

Jake has a quick and dirty shell script in bash which runs this. It downloads and unzips file, creates a folder. Each text file is an email. They put spam and ham in separate folders.

Jake uses “wc” to count the number of messages for one former Enron employee, for example. He sees 1500 spam, and 3672 ham. Using grep, he counts the number of instances of “meeting”:

grep -il meeting enron1/spam/*.txt | wc -l

This gives 153. This is one of the handful of computations we need to compute

Note we don’t need a fancy programming environment to get this done.

Next, we try:

• “money”: 80% chance of being spam.
• “viagra”: 100% chance.
• “enron”: 0% chance.

This illustrates overfitting; we are getting overconfident because of our biased data. It’s possible, in other words, to write an non-spam email with the word “viagra” as well as a spam email with the word “enron.”

Next, do it for all the words. Each document can be represented by a binary vector, whose jth entry is 1 or 0 depending whether jth word appears. Note this is a huge-ass vector, we will probably actually represent it with the indices of the words that actually do show up.

Here’s the model we use to estimate the probability that we’d see a given word vector given that we know it’s spam (or that it’s ham). We denote the document vector and the various entries , where the correspond to all the indices of in other words over all the words. For now we denote “is spam” by :

The theta here is the probability that an individual word is present in a spam email (we can assume separately and parallel-ly compute that for every word). Note we are modeling the words independently and we don’t count how many times they are present. That’s why this is called “Naive”.

Let’s take the log of both sides:

[It’s good to take the log because multiplying together tiny numbers can give us numerical problems.]

The term doesn’t depend on a given document, just the word, so let’s rename it Same with . The real weights that vary by document are the ‘s.

We can now use Bayes’ Rule to get an estimate of which is what we actually want. We can also get away with not computing all the terms if we only care whether it’s more likely to be spam or to be ham. Only the varying term needs to be computed.

Wait, this ends up looking like a linear regression! But instead of computing them by inverting a huge matrix, the weights come from the Naive Bayes’ algorithm.

This algorithm works pretty well and it’s “cheap to train” if you have pre-labeled data set to train on. Given a ton of emails, just count the words in spam and non-spam emails. If you get more training data you can easily increment your counts. In practice there’s a global model, which you personalize to individuals. Moreover, there are lots of hard-coded, cheap rules before an email gets put into a fancy and slow model.

Here are some references:

• “Idiot’s Bayes – not so stupid after all?” – the whole paper is about why it doesn’t suck, which is related to redundancies in language.
• “Naive Bayes at Forty: The Independence Assumption in Information“
• “Spam Filtering with Naive Bayes – Which Naive Bayes?“

Laplace Smoothing

Laplace Smoothing refers to the idea of replacing our straight-up estimate of the probability of seeing a given word in a spam email with something a bit fancier:

We might fix and for example, to prevents the possibility of getting 0 or 1 for a probability. Does this seem totally ad hoc? Well if we want to get fancy, we can see this as equivalent to having a prior and performing a maximal likelihood estimate.

If we denote by the maximal likelihood estimate, then we have:

In other words, we are asking the question, for what value of were the data D most probable? If we assume independent trials then we want to maximize

If you take the derivative, and set it to zero, we get

In other words, just what we had before. Now let’s add a prior. Denote by the maximum a posteriori likelihood:

This similarly asks the question, given the data I saw, which parameter is the most likely?

Use Bayes’ rule to get . This looks similar to above except for the , which is the “prior”. If I assume is of the form ; then we get the above, Laplacian smoothed version.

Sometimes and are called “pseudo counts”. They’re fancy but also simple. It’s up to the data scientist to set the values of these hyperparameters, and it gives us two knobs to tune. By contrast, k-nearest neighbors has one knob, namely k.

Note: In the last 5 years people have started using stochastic gradient methods to avoid the non-invertible (overfitting) matrix problem. Switching to logistic regression with stochastic gradient method helped a lot, and can account for correlations between words. Even so, Naive Bayes’ is pretty impressively good considering how simple it is.

Scraping the web: API’s

For the sake of this discussion, an API (application programming interface) is something websites provide to developers so they can download data from the website easily and in standard format. Usually the developer has to register and receive a “key”, which is something like a password. For example, the New York Times has an API here. Note that some websites limit what data you have access to through their API’s or how often you can ask for data without paying for it.

When you go this route, you often get back weird formats, sometimes in JSON, but there’s no standardization to this standardization, i.e. different websites give you different “standard” formats.

One way to get beyond this is to use Yahoo’s YQL language which allows you to go to the Yahoo! Developer Network and write SQL-like queries that interact with many of the common API’s on the common sites like this:

select * from flickr.photos.search where text=”Cat” and api_key=”lksdjflskjdfsldkfj” limit 10

The output is standard and I only have to parse this in python once.

What if you want data when there’s no API available?

Note: always check the terms and services of the website before scraping.

In this case you might want to use something like the Firebug extension for Firefox, you can “inspect the element” on any webpage, and Firebug allows you to grab the field inside the html. In fact it gives you access to the full html document so you can interact and edit. In this way you can see the html as a map of the page and Firebug is a kind of tourguide.

After locating the stuff you want inside the html, you can use curl, wget, grep, awk, perl, etc., to write a quick and dirty shell script to grab what you want, especially for a one-off grab. If you want to be more systematic you can also do this using python or R.

Other parsing tools you might want to look into:

• lynx and lynx –dump: good if you pine for the 1970’s. Oh wait, 1992. Whatever.
• Beautiful Soup: robust but kind of slow
• Mechanize (or here) super cool as well but doesn’t parse javascript.

Postscript: Image Classification

How do you determine if an image is a landscape or a headshot?

You either need to get someone to label these things, which is a lot of work, or you can grab lots of pictures from flickr and ask for photos that have already been tagged.

Represent each image with a binned RGB – (red green blue) intensity histogram. In other words, for each pixel, for each of red, green, and blue, which are the basic colors in pixels, you measure the intensity, which is a number between 0 and 255.

Then draw three histograms, one for each basic color, showing us how many pixels had which intensity. It’s better to do a binned histogram, so have counts of # pixels of intensity 0 – 51, etc. – in the end, for each picture, you have 15 numbers, corresponding to 3 colors and 5 bins per color. We are assuming every picture has the same number of pixels here.

Finally, use k-nearest neighbors to decide how much “blue” makes a landscape versus a headshot. We can tune the hyperparameters, which in this case are # of bins as well as k.