mathbabe

This is a continuation of this, where I take notes on my workshop at HCSSiM.

Aaron was visiting my class yesterday and talked about Sandpiles. Here are his notes:

Sandpiles: what they are

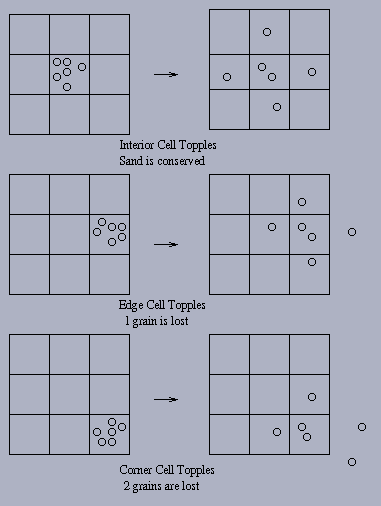
For fixed , an beach is a grid with some amount of sand in each spot. If there is too much sand in one place, it topples, sending one grain of sand to each of its neighbors (thereby losing 4 grains of sand). If this happens on an edge of the beach, one of the grains of sand falls off the edge and is gone forever. If it happens at a corner, 2 grains are lost. If there’s no toppling to do, the beach is stable. Here’s a 3-by-3 example I stole from here:

Do stable beaches form a group?

Answer: well, you can add them together (pointwise) and then let that stabilize until you’ve got back to a stable beach (not trivial to prove this always settles! But it does). But is the sum well-defined?

In other words, if there is a cascade of toppling, does it matter what order things topple? Will you always reach the same stable beach regardless of how you topple?

Turns out the answer is yes, if you think about these grids as huge vectors and toppling as adding other 2-dimensional vectors with a ‘-4’ in one spot, a ‘1’ in each of the four spots neighboring that, and ‘0’ elsewhere. It inherits commutativity from addition in the integers.

Wait! Is there an identity? Yep, the beach with no sand; it doesn’t change anything when you add it.

Wait!! Are there inverses? Hmmmmm….

Lemma: There is no way to get back to all 0’s from any beach that has sand.
Proof. Imagine you could. Then the last topple would have to end up with no sand. But every topple adds sand to at least 2 sites (4 if the toppling happens in the center, 3 if on an edge, 2 if on a corner). Equivalently, nothing will topple unless there are at least 4 grains of sand total, and toppling never loses more than 2 grains, so you can never get down to 0.

Conclusion: there are no inverses; you cannot get back to the ‘0’ grid from anywhere. So it’s not a group.

Try again

Question: Are there beaches that you can get back to by adding sand?

There are: on a 2-by-2 beach, the ‘2’ grid (which means a 2 in every spot) plus itself is the ‘4’ grid, and that topples back to the ‘2’ grid if you topple every spot once. Also, the ‘2’ grid adds to the grid and gets it back.

Wow, it seems like the ‘2’ grid is some kind of additive identity, at least for these two elements. But note that the ‘1’ grid plus the ‘2’ grid is the ‘3’ grid, which doesn’t topple back to the ‘1’ grid. So the ‘2’ grid doesn’t work as an identity for everything.

We need another definition.

Recurrent sandpiles

A stable beach C is recurrent if (i) it is stable, and (ii) given any beach A, there is a beach B such that C is the stabilization of A+B. We just write this C = A+B but we know that’s kind of cheating.

Alternative definition: a stable beach C is recurrent if (i) it is stable, and (ii) you can get to C by starting at the maximum ‘3’ grid, adding sand (call that part D), and toppling until you get something stable. C = ‘3’ + D.

It’s not hard to show these definitions are equivalent: if you have the first, let A = ‘3’. If you have the second, and if A is stable, write A + A’ = ‘3’, and we have B = A’ + D. Then convince yourself A doesn’t need to be stable.

Letting A=C we get a beach E so C = C+E, and E looks like an identity.

It turns out that if you have two recurrent beaches, then if you can get back to one using a beach E then you can get back to to the other using that same beach E (if you look for the identity for C + D, note that (C+D)+E = (C+E) + D = C+D; all recurrent beaches are of the form C+D so we’re done). Then that E is an identity element under beach addition for recurrent beaches.

Is the identity recurrent? Yes it is (why? this is hard and we won’t prove it). So you can also get from A to the identity, meaning there are inverses.

The recurrent beaches form a group!

What is the identity element? On a 2-by-2 beach it is the ‘2’ grid. The fact that it didn’t act as an identity on the ‘1’ grid was caused by the fact that the ‘1’ grid isn’t itself recurrent so isn’t considered to be inside this group.

Try to guess what it is on a 2-by-3 beach. Were you right? What is the order of the ‘2’ grid as a 2-by-3 beach?

Try to guess what the identity looks like on a 198-by-198 beach. Were you right? Here’s a picture of that:

We looked at some identities on other grids, and we watched an app generate one. You can play with this yourself. (Insert link).

The group of recurrent beaches is called the m-by-n sandpile group. I wanted to show it to the kids because I think it is a super cool example of a finite commutative group where it is hard to know what the identity element looks like.

You can do all sorts of weird things with sandpiles, like adding grains of sand randomly and seeing what happens. You can even model avalanches with this. There’s a sandpile applet you can go to and play with.