HCSSiM Workshop day 16

Home > math education > HCSSiM Workshop day 16

HCSSiM Workshop day 16

July 20, 2012 Cathy O'Neil, mathbabe

This is a continuation of this, where I take notes on my workshop at HCSSiM.

Two days ago Benji Fisher came to my workshop to talk about group laws on rational points of weird things in the plane. Here are his notes.

Degenerate Elliptic Curves in the plane

Conics in the plane

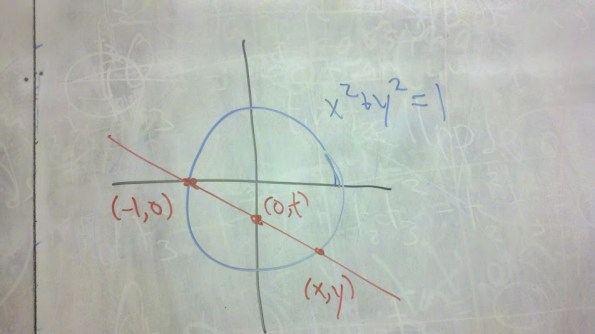
Pick $t \in \mathbb{R}$ . Consider the line $L_t$ given by $y = tx + t$ . Where does $L_t$ intersect the y-axis? Where does it intersect the unit circle, $x^2 + y^2 =1?$

Substitute $y = tx +t$ into the equation for the circle to get

$(1 + t^2) \, x^2 + (2 t^2) \, x + (t^2 - 1) = 0.$

After you do it the hard way, notice that you already know one root: $x = -1$ .

The sum of the roots is $-2 t^2 / (1 + t^2)$ and their product is $(t^2 - 1) / (t^2 + 1)$ . Either way, you get

$x = (1 - t^2) / (1 + t^2)$ .

From $y= t x + t$ you get $y = 2 t / (1 + t^2)$ .

Do not forget that if you are given $x$ and $y$ , then $t = y / (x + 1)$ .

This gives you a 1-1 correspondence between the points of the circle (conic) and the points of the $y$ -axis (including $\infty$ ). The formula for Pythagorean triples also falls out. So do the formulae for the tangent-of-the-half-angle substitution, which is useful when integrating rational functions of $\sin$ and $\cos$ : set $x = \cos(\theta),$ $y = \sin(\theta),$ and $t = \tan(\theta/2).$

There are several ways you can generalize this. You could project a sphere onto a plane. I want to consider replacing the circle with a cubic curve. The problem is that the expected number of intersections between a line and a cubic is 3, so you get a 2-to-1 correspondence in general. That is interesting, too, but for now I want to consider the cases where the curve has a double point and I choose lines through that point. Such lines should intersect the cube in one other point, giving a 1-1 correspondence between the curve (minus the singular point) and a line (minus a small number of points).

cubic with a cusp

Let $C$ be the curve defined by

$y^2 = x^3$ ,

which has a sharp corner at the origin. This type of singularity is called a cusp. Let $L_t$ denote the line through the origin and the point $(1,t)$ , which has slope $t$ .

Sketch the curve $C$ . Does Mathematica do a good job of this?
The line $L_t$ meets the curve $C$ at the origin and in one other point, $(x, y)$ . Find formulae for $x$ and $y$ in terms of $t$ and for $t$ in terms of $x$ and $y$ .
You almost get a digestion (bijection) between $C$ and the line $x = 1$ . What points do you have to omit from each in order to get a digestion?
Three points $(x_1, y_1), (x_2, y_2)$ , and $(x_3, y_3)$ on $C$ are collinear. What condition does this impose on the corresponding values of $t$ ?

The calculations are easier than for the circle: $x=t^2, y = t^3$ , and $t = y/x.$

You have to remove the point $(0, 0)$ from the curve and the point $(1, 0)$ from the line. Well, you do not have to remove them, but the formula for $t$ in terms of $x$ and $y$ is fishy if you do not. The point at infinity (the third point of intersection between the curve and the $y$ -axis) corresponds to itself.

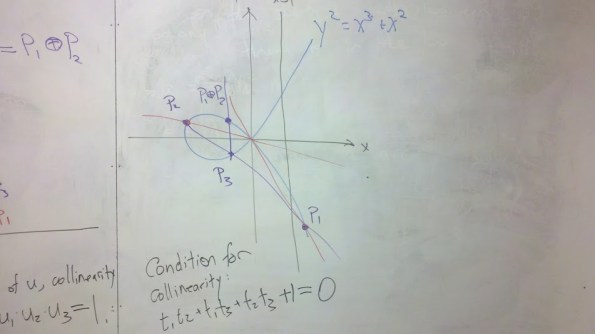
The condition for colliniarity is

$\frac{y_3 - y_1}{x_3 - x_1} = \frac{y_2 - y_1}{x_2 - x_1}.$

Plug in the expressions in terms of the $t$ coordinates, chug away, and you should get

$t_1^{-1} + t_2^{-1} + t_3^{-1} = 0$ .

If we let $u = t^{-1}$ , then $u$ is the natural coordinate on the line $y=1$ . (Maybe I should use that line to start with instead of $x=1$ .)

cubic with a node

This problem deals with the curve $C$ defined by

$y^2 = x^3 + x^2$ ,

which intersects itself at the origin. This type of singularity is called a node. Let $L_t$ denote the line through the origin and the point $(1,t)$ , which has slope $t$ .

Sketch the curve $C$ . Does Mathematica do a good job of this?
The line $L_t$ meets the curve $C$ at the origin and in one other point, $(x, y$ ). Find formulae for $x$ and $y$ in terms of $t$ and for $t$ in terms of $x$ and $y$ .
You almost get a digestion (bijection) between $C$ and the line $x = 1$ . What points do you have to omit from each in order to get a digestion?
Three points $(x_1, y_1), (x_2, y_2)$ , and $(x_3, y_3)$ on $C$ are collinear. What condition does this impose on the corresponding values of $t$ ?

Once again, $t = y / x$ . The usual method gives $x = t^2 - 1$ and $y = t^3 - t$ . In order to get a 1-1 correspondence, you need to delete the singular point $(0,0)$ from the curve and the points $(1,1)$ and $(1,-1)$ from the line.

The lines through the origin with slope $\pm1$ are tangent to the curve. If you plug away, you should find that the condition for colliniarity is:

$t_1 t_2 + t_1 t_3 + t_2 t_3 + 1 = 0$ .

Remember our curve $C$ (not to be Maximum Confused with $\mathbb{C}$ )? It’s the one whose equation is $u^2 = x^3 + x^2.$ The condition for 3 points to be collinear on $C$ is:

$t_1 t_2 + t_2 t_3 + t_3 t_1 +1 = 0.$

Claim: in terms of $u = \frac{t-1}{t+1}$ , the condition is $u_1 u_2 u_3 = 1.$

(Hint: In terms of $u$ , $t = \frac{1+u}{1 - u}$ .)

If you start with the known equation and replace the $t$ ‘s with $u$ ‘s, it takes some work to get down to the condition $u_1 u_2 u_3 = 1$ .

If you start with the LHS of the desired equation, there is a shortcut:

$u_1 u_2 u_3 = \frac{t_1 - 1}{t_1 + 1} \cdot \frac{t_2 - 1}{t_2 + 1}$ $\cdot \frac{t_3-1}{t_3+1}$ .

But then we have

$u_1 u_2 u_3 = \frac{t_1 t_2 t_3 + t_1 + t_2 + t_3 - (t_1 t_2 + t_1 t_3 + t _2 t_3 + 1)}{t_1 t_2 t_3 + t_1 + t_2 + t_3 + (t_1 t_2 + t_2 t_3 + t_3 t_1 + 1)} = 1.$

Note that the change-of-variable formulae are fractional linear transformations. Geometrically, $t$ is the natural coordinate on the line $x=1$ and $u$ is the natural coordinate on the line $x + y = 1$ .

To get from one line to the other, just draw a line through the origin.

One interpretation of our results for the curves $y^2 = x^3$ , $y^2 = x^3 + x^2$ , is that it gives us a way to add points on the line $y = 1$ (with coordinate $t^{-1}$ ) and multiply points on the line $x + y = 1$ (with coordinate $u$ ) using just a straightedge, provided that we are allowed to draw lines through the point at infinity.

In other words, we are allowed to draw vertical lines. I will continue to refer to this as “straightedge only.” I forgot to mention: you need to have the curve provided as well. Explicitly, this is the rule. Given two points on the line, find the corresponding point on the curve. Draw a line through them. The third point of intersection with the curve will be the (additive or multiplicative) inverse of the desired sum. Draw a vertical line through this point: the second point of intersection (or the third, if you count the point at infinity as being the second) will be the desired sum/product.

More precisely, it is the point on the curve corresponding to the desired sum/product, so you have to draw one more line.

Another interpretation is that we get a troupe (or karafiol) structure on the points of the curve, excluding the singular point but including the point at infinity. The point at infinity is the identity element of the troupe (group). The construction is exactly the same as in the previous paragraph, except you leave off the parts about starting and ending on the line.

smooth cubic

Similarly, we get a troupe (group) structure on any smooth cubic curve. For example, consider the curve $E$ defined by

$E: y^2 = x^3 - x .$

Start with two points on the curve, say $P_1 = (x_1, y_1)$ and $P_2 = (x_2, y_2)$ . The equation for the line through these two points is $\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1} = m .$ $

Solving for $y$ gives the equation $y = mx + b$ where $b = \frac{x_2 y_1 - x_1 y_2}{x_2 - x_1}.$

Plug this into the equation defining $R$ and you get, after a little algebra,

$x^3- m^2 x^2 - (2 m b + 1)x - b^2 = 0 .$

Luckily, we know how to solve the general cubic. (Just kidding! Coming back to what we did with the circle, we observe that $x_1$ and $x_2$ are two of the roots, so we can use either of the relations $x_1 + x_2 + x_3 = m^2$ or $x_1 x_2 x_3 = b^2$ .)

The result is:

$x_3 = m^2 - x_1 - x_2 = \frac{x_1^2 x_2 + x_1 x_2^2 - x_1 - x_2 - 2 y_1 y_2}{(x_1 - x_2)^3},$

where the final form comes from squaring $m$ and using the relations $y_1^2 = x_1^3 - x_1$ and $y_2^2 = x_2^3 - x_2$ .

At this point, a little patience (or a little computer-aided algebra) gives

$y_3 = \frac{(3 x_1 x_2^2 + x_2^3 - x_1 - 3 x_2) y_1 + (-x_1^3 - 3 x_1^2 x_2 + 3 x_1 + x_2) y_2}{(x_1 - x_2)^3}.$

Do not forget the final step: $P_3 = (x_3, y_3)$ is the third point of intersection, but to get the sum we need to draw a vertical line, or reflect in the $x$ -axis:

$P_1 \oplus P_2 = \overline{P_3} = (x_3, - y_3).$

Now, I give up. With a lot of machinery, I could exlpain why the group law is associative. (The identity, as I think I said above, is the point at infinity. Commutativity and inverses are clear.) What I can do with a different machine (Mathematica or some other computer-algebra system) is verify the associative law. I could also do it by hand, given a week, but I do not think I would learn anything from that exercise.

Some content on this page was disabled on December 15, 2019.

Categories: math education

Comments (1)

Benji

July 22, 2012 at 9:30 pm

Given the poor organization of the notes, not to mention a little unusual terminology, I want to explain the context of the notes that Cathy posted here. I talked about these ideas over several days, and several problem sets, in my own class before giving a single presentation in Cathy’s. In case she and her junior staff wanted to follow up in her own p-sets, I copied several problems into one document and added enough commentary that Cathy (who was returning the favor while I talked in her class) would know the context and would have an easy reference for the answers.

As for the unusual terminology, Cathy must have explained that elsewhere …

One further note. Since the group law on the smooth points of the cuspidal and nodal cubics corresponds to addition and multiplication (respectively) on the number line, we get associativity for free. For the smooth cubic, we have to verify associative law, but the reward is that we get a brand-new group. (If some smart alec wants to say the group is not new because of the parameterization in terms of elliptic functions, I have a ready defense: finite fields!)

LikeLike