Archive
Back from Strata Jumpstart
So I gave my talk yesterday at the Strata Jumpstart conference, and I’ll be back on Thursday and Friday to attend the Strata Conference conference.
I was delighted to meet a huge number of fun, hopeful, and excited nerds throughout the day. Since my talk was pretty early in the morning, I was able to relax afterwards and just enjoy all the questions and remarks that people wanted to discuss with me.
Some were people with lots of data, looking for data scientists who could analyze it for them, others were working with packs of data scientists (herds? covens?) and were in search of data. It was fun to try to help them find each other, as well as to hear about all the super nerdy and data-driven businesses that are getting off the ground right now. It certainly was an optimistic tone, I didn’t feel like we were in the middle of a double-dip recession for the entire day (well, at least til I got home and looked at the Greek default news).
Conferences like these are excellent; they allow people to get together and learn each others’ languages and the existence of the new tools and techniques in use or in development. They also save people lots of time, make fast connection that would otherwise difficult or impossible, and of course sometimes inspire great new ideas. Too bad they are so expensive!
I also learned that there’s such thing as a “data scientist in residence,” held of course by very few people, which is the equivalent in academic math to having a gig at the Institute for Advanced Study in Princeton. Wow. I still haven’t decided whether I’d want such a cushy job. After all, I think I learn the most when I have reasonable pressure to get stuff done with actual data. On the other hand maybe that much freedom would allow one to do really cool stuff. Dunno.
The pandas module and the IPython notebook
Last night I attended this Meetup on a cool package that Wes McKinney has been writing (in python and in cython, which I guess is like python but is as fast as c). That guys has been ridiculously prolific in his code, and we can all thank him for it, because pandas looks really useful.
To sum up what he’s done: he’s imported the concept of the R dataframe into python, with SQL query-like capabilities as well, and potentially with some map-reduce functionality, although he hasn’t tested it on huge data. He’s also in the process of adding “statsmodel” functionality to the dataframe context (he calls a dataframe a Series), with more to come soon he’s assured us.
So for example he demonstrated how quickly one could regress various stocks against each other, and if we had a column of dates and months (so actually hierarchical labels of the data), then you could use a “groupby” statement to regress within each month and year. Very cool!
He demonstrated all of this within his IPython Notebook, which seems to demonstrate lots of what I liked when I learned about Elastic-R (though not all, like the cloud computing part of Elastic-R is just awesome), namely the ability to basically send your python session to someone like a website url and to collaborate. Note, I just saw the demo I can’t speak from personal experience, but hopefully I will be able to soon! It’s a cool way to remotely use a powerful machine and not need to worry about your local setup.
Monday morning links
First, if you know and love the Statistical Abstract as much as I do, then help save it! Go to this post and follow the instructions to appeal to the census to not discontinue its publication.
Next, if you want evidence that it sucks to be rich, or at least it sucks to be a child of rich people, then read this absolutely miserable article about how rich people control and manipulate their children. Note the entire discussion about “problem children” never discusses the possibility that you are actually a lousy, money-obsessed and withholding parent.
Next, how friggin’ cool is this? Makes me want to visit Mars personally.
And also, how cool is it that the World Bank is opening up its data?
Finally, good article here about Bernanke’s lack of understanding of reality.
Meetups
I wanted to tell you guys about Meetup.com, which is a company that helps people form communities to share knowledge and techniques as well as to have pizza and beer. It’s kind of like taking the best from academics (good talks, interested and nerdy audience) and adding immediacy and relevance; I’ve been using stuff I learned at Meetups in my daily job.
I’m involved in three Meetup groups. The first is called NYC Machine Learning, and they hold talks every month or so which are technical and really excellent and help me learn this new field, and in particular the vocabulary of machine learners. For example at this recent meeting, on the cross-entropy method.
The second Meetup group I go to is called New York Open Statistical Programming Meetup, and there the focus is more on recent developments in open source programming languages. It’s where I first heard of Elastic R for example, and it’s super cool; I’m looking forward to this week’s talk entitled “Statistics and Data Analysis in Python with pandas and statsmode“. So as you can see the talks really combine technical knowledge with open source techniques. Very cool and very useful, and also a great place to meet other nerdy startuppy data scientists and engineers.
The third Meetup group I got to is called Predictive Analytics. Next month they’re having a talk to discuss Bayesians vs. frequentists, and I’m hoping for a smackdown with jello wrestling. Don’t know who I’ll root for, but it will be intense.
Some cool links
First, right on the heels of my complaining about publicly available data being unusable, let me share this link, which is a FREAKING cool website which allows people to download 2010 census data in a convenient and usable form, and also allows you to compare those numbers to the 2000 census. It allows you to download it directly, or by using a url, or via SQL, or via Github. It was created by a group called Investigative Reporters and Editors (IRE) for other journalists to use. That is super awesome and should be a model for other people providing publicly available data (SEC, take notes!).
Next, I want you guys to know about stats.org, which is a fantastic organization which “looks at major issues and news stories from a quantitative and scientific perspective.” I always find something thought-provoking and exciting when I go to their website. See for example their new article on nature vs. nurture for girls in math. Actually I got my hands on the original paper about this and I plan to read it and post my take soon (thanks, Matt!). Also my friend Rebecca Goldin is their Director of Research (and is featured in the above article) and she rocks.
Along the same lines, check out straightstatistics.org which is based in the UK and whose stated goal is this: “we are a campaign established by journalists and statisticians to improve the understanding and use of statistics by government, politicians, companies, advertisers and the mass media. By exposing bad practice and rewarding good, we aim to restore public confidence in statistics. which checks the statistics behind news and politics.” Very cool.
What is “publicly available data”?
As many of you know, I am fascinated with the idea of an open source ratings model, set up to compete with the current big three ratings agencies S&P, Moody’s, and Fitch. Please check out my previous posts here and here about this idea.
For that reason, I’ve recently embarked on the following thought experiment: what would it take to start such a thing? As is the case with most things quantitative and real-world, the answer is data. Lots of it.
There’s good news and bad news. The good news is there are perfectly reasonable credit models that use only “publicly available data”, which is to say data that can theoretically gleaned from quarterly filings that companies are required to file. The bad news is, the SEC filings, although available on the web, are completely useless unless you have a team of accounting professionals working with you to understand them.
Indeed what actually happens if you work at a financial firm and want to implement a credit model based on “publicly available information” is the following: you pay a data company like Compustat good money for a clean data feed to work with. They charge a lot for this, and for good reason: the SEC doesn’t require companies to standardize their accounting terms, even within an industry, and even over time (so the same company can change the way it does its accounting from quarter to quarter). Here‘s a link for the white paper (called The Impact of Disparate Data Standardization on Company Analysis) which explains the standardization process that they go through to “clean the data”. It’s clearly a tricky thing requiring true accounting expertise.
To sum up the situation, in order to get “publicly available data” into usable form we need to give a middle-man company like Compustat thousands of dollars a year. Wait, WTF?!!? How is that publicly available?
And who is this benefitting? Obviously it benefits Compustat itself, in that there even is a business to be made from converting publicly available data into usable data. Next, it obviously benefits the companies to not have to conform to standards- easier for them to hide stuff they don’t like (this is discussed in the first section of Compustat’s whitepaper referred to above), and to have options each quarter on how the presentation best suits them. So… um… does it benefit anyone besides them? Certainly not any normal person who wants to understand the creditworthiness of a given company. Who is the SEC working for anyway?
I’ve got an idea. We should demand publicly available data to be usable. Standard format, standard terminology, and if there are unavoidable differences across industries (which I imagine there are, since some companies store goods and others just deal in information for example), then there should be fully open-source translation dictionaries written in some open-source language (python!) that one can use to standardize the overall data. And don’t tell me it can’t be done, since Compustat already does it.
SEC should demand the companies file in a standard way. If there really are more than a couple of standard terms, then demand the company report in each standard way. I’m sure the accountants of the company have this data, it’s just a question of requiring them to report it.
Back!
I’m back from vacation, and the sweet smell of blog has been calling to me. Big time. I’m too tired from Long Island Expressway driving to make a real post now, but I have a few things to throw your way tonight:
First, I’m completely loving all of the wonderful comments I continue to receive from you, my wonderful readers. I’m particularly impressed with the accounting explanation on my recent post about the IASP and what “level 3” assets are. Here is a link to the awesome comments, which has really turned into a conversation between sometimes guest blogger FogOfWar and real-life accountant GMHurley who knows his shit. Very cool and educational.
Second, my friend and R programmer Daniel Krasner has finally buckled and started a blog of his very own, here. It’s a resource for data miners, R or python programmers, people working or wanting to work at start-ups, and thoughtful entrepreneurs. In his most recent post he considers how smart people have crappy ideas and how to focus on developing good ones.
Finally, over vacation I’ve been reading anarchist David Graeber‘s new book about debt, and readers, I think I’m in love. In a purely intellectual and/or spiritual way, of course, but man. That guy can really rile me up. I’ll write more about his book soon.
Strata data conference
So I’m giving a talk at this conference. I’m talking on Monday, September 19th, to business people, about how they should want to hire a data scientist (or even better, a team of data scientists) and how to go about hiring someone awesome.
Any suggestions?
And should I wear my new t-shirt when I’m giving my talk? Part of the proceeds of these sexy and funny data t-shirts goes to Data Without Borders! A great cause!
Lagged autocorrelation plots
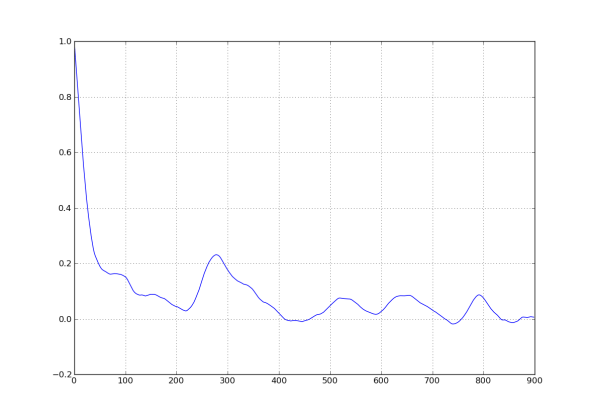
I wanted to share with you guys a plot I drew with python the other night (the code is at the end of the post) using blood glucose data that I’ve talked about previously in this post and I originally took a look at in this post.
First I want to motivate lagged autocorrelation plots. The idea is, given that you want to forecast something, say in the form of a time series (so a value every day or every ten minutes or whatever), the very first thing you can do is try to use past values to forecast the next value. In other words, you want to squeeze as much juice out of that orange as you can before you start using outside variable to predict future values.
Of course this won’t always work- it will only work, in fact, if there’s some correlation between past values and future values. To estimate how much “signal” there is in such an approach, we draw the correlation between values of the time series for various lags. At no (=0) lag, we are comparing a time series to itself so the correlation is perfect (=1). Typically there are a few lags after 0 which show some positive amount of correlation, then it quickly dies out.
We could also look at correlations between returns of the values, or differences of the values, in various situations. It depends on what you’re really trying to predict: if you’re trying to predict the change in value (which is usually what quants in finance do, since they want to bet on stock market changes for example), probably the latter will make more sense, but if you actually care about the value itself, then it makes sense to compute the raw correlations. In my case, since I’m interested in forecasting the blood glucose levels, which essentially have maxima and minima, I do care about the actual number instead of just the relative change in value.
Depending on what kind of data it is, and how scrutinized it is, and how much money can be made by betting on the next value, the correlations will die out more quickly. Note that, for example, if you did this with daily S&P returns and saw a nontrivial positive correlation after 1 lag, so the next day, then you could have a super simple model, namely bet that whatever happened yesterday will happen again today, and you would statistically make money on that model. At the same time, it’s a general fact that as “the market” recognizes and bets on trends, they tend to disappear. This means that such a simple, positive one-day correlation of returns would be “priced in” very quickly and would therefore disappear with new data. This tends to happen a lot with quant models- as the market learns the model, the predictability of things decreases.
However, in cases where there’s less money riding on the patterns, we can generally expect to see more linkage between lagged values. Since nobody is making money betting on blood glucose levels inside someone’s body, I had pretty high hopes for this analysis. Here’s the picture I drew:
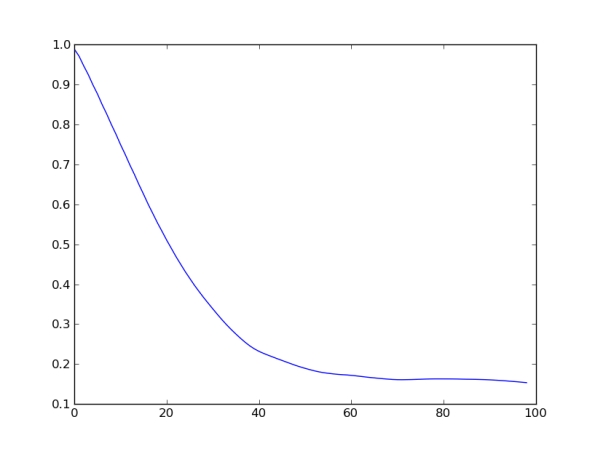
What do you see? Basically I want you to see that the correlation is quite high for small lags, then dies down with a small resuscitation near 300 (hey, it turns out that 288 lags equals one day! So this autocorrelation lift is probably indicating a daily cyclicality of blood glucose levels). Here’s a close-up for the first 100 lags:
We can conclude that the correlation seems significant to about 30 lags, and is decaying pretty linearly.
This means that we can use the previous 30 lags to predict the next level. Of course we don’t want to let 30 parameters vary independently- that would be crazy and would totally overfit the model to the data. Instead, I’ll talk soon about how to place a prior on those 30 parameters which essentially uses them all but doesn’t let them vary freely- so the overall number of independent variables is closer to 4 or 5 (although it’s hard to be precise).
On last thing: the data I have used for this analysis is still pretty dirty, as I described here. I will do this analysis again once I decide how to try to remove crazy or unreliable readings that tend to happen before the blood glucose monitor dies.
Here’s the python code I used to generate these plots:
#!/usr/bin/env python
import csv
from matplotlib.pylab import *
import os
from datetime import datetime
os.chdir('/Users/cathyoneil/python/diabetes/')
gap_threshold = 12
dataReader = csv.DictReader(open('Jason_large_dataset.csv', 'rb'), delimiter=',', quotechar='|')
i=0
datelist = []
datalist = []
firstdate = 4
skip_gaps_datalist = []
for row in dataReader:
#print i, row["Sensor Glucose (mg/dL)"]
if not row["Raw-Type"] == "GlucoseSensorData":continue
if firstdate ==4:
print i
firstdate = \
datetime.strptime(row["Timestamp"], '%m/%d/%y %H:%M:%S')
if row["Sensor Glucose (mg/dL)"] == "":
datalist.append(-1)
else:
thisdate = datetime.strptime(row["Timestamp"], '%m/%d/%y %H:%M:%S')
diffdate = thisdate-firstdate
datelist.append(diffdate.seconds + 60*60*24*diffdate.days)
datalist.append(float(row["Sensor Glucose (mg/dL)"]))
skip_gaps_datalist.append(log(float(row["Sensor Glucose (mg/dL)"])))
i+=1
continue
print min(datalist), max(datalist)
##figure()
##scatter(arange(len(datalist)), datalist)
##
##figure()
##hist(skip_gaps_datalist, bins = 100)
##show()
def lagged_correlation(g):
d = dict(zip(datelist, datalist))
s1 = []
s2 = []
for date in datelist:
if date + 60*5 in datelist:
s1.append(d[date])
s2.append(d[date + 60*5])
return corrcoef(s1, s2)[1, 0]
figure()
plot([lagged_correlation(f) for f in range(1,900)])
What’s with errorbars?
As an applied mathematician, I am often asked to provide errorbars with values. The idea is to give the person reading a statistic or a plot some idea of how much the value or values could be expected to vary or be wrongly estimated, or to indicate how much confidence one has in the statistic. It’s a great idea, and it’s always a good exercise to try to provide the level of uncertainty that one is aware of when quoting numbers. The problem is, it’s actually very tricky to get them right or to even know what “right” means.
A really easy way to screw this up is to give the impression that your data is flawless. Here’s a prime example of this.
More recently we’ve seen how much the government growth rate figures can really suffer from lack of error bars- the market reacts to the first estimate but the data can be revised dramatically later on. This is a case where very simple errorbars (say, showing the average size of the difference between first and final estimates of the data) should be provided and could really help us gauge confidence. [By the way, it also brings up another issue which most people think about as a data issue but really is just as much a modeling issue: when you have data that gets revised, it is crucial to save the first estimates, with a date on that datapoint to indicate when it was first known. If we instead just erase the old estimate and pencil in the new, without changing the date (usually leaving the first date), then it gives us a false sense that we knew the “corrected” data way earlier than we did.]
However, even if you don’t make stupid mistakes, you can still be incredibly misleading, or misled, by errorbars. For example, say we are trying to estimate risk on a stock or a portfolio of stocks. Then people typically use “volatility error bars” to estimate the expected range of values of the stock tomorrow, given how it’s been changing in the past. As I explained in this post, the concept of historical volatility depends crucially on your choice of how far back you look, which is given by a kind of half-life, or equivalently the decay constant. Anything that is so not robust should surely be taken with a grain of salt.
But in any case, volatility error bars, which are usually designed to be either one or two lengths of the measured historical volatility, contain only as much information as the data in the lookback window. In particular, you can get extremely confused if you assume that the underlying distribution of returns is normal, which is exactly what most people do in fact assume, even when they don’t realize they do.
To demonstrate this phenomenon of human nature, recall that during the credit crisis you’d hear things like “We were seeing things that were 25-standard deviation moves, several days in a row,” from Goldman Sachs; the implication was that this was an incredibly unlikely event, near probability zero in fact, that nobody could have foreseen. Considering what we’ve been seeing in the market in the past couple of weeks, it would be nice to understand this statement.
There were actually two flawed assumptions exposed here. First, if we have a fat-tailed distribution, then things can seem “quiet” for long stretches of time (longer than any lookback window), during which the sample volatility is a possibly severe underestimate of the standard of deviation. Then when a fat-tailed event occurs, the sample volatility spikes to being an overestimate of the standard of deviation for that distribution.
Second, in the markets, there is clustering of volatility- another way of saying this is that volatility itself is rather auto-correlated, so even if we can’t predict the direction of the return, we can still estimate the size of the return. So once the market dives 5% in one day, you can expect many more days of large moves.
In other words, the speaker was measuring the probability that we’d see several returns, 25 standard deviations away from the mean, if the distribution is normal, with a fixed standard deviation, and the returns are independent. This is indeed a very unlikely event. But in fact we aren’t dealing with normal distributions nor independent draws.
Another way to work with errorbars is to have confidence errorbars, which relies (explicitly or implicitly) on an actual distributional assumption of your underlying data, and which tells the reader how much you could expect the answer to range given the amount of data you have, with a certain confidence. Unfortunately, there are problems here too- the biggest one being that there’s really never any reason to believe your distributional assumptions beyond the fact that it’s probably convenient, and that so far the data looks good. But if it’s coming from real world stuff, a good level of skepticism is healthy.
In another post I’ll talk a bit more about confidence errorbars, otherwise known as confidence intervals, and I’ll compare them to hypothesis testing.
Open Source Ratings Model (Part 2)
I’ve thought more about the concept of an open source ratings model, and I’m getting more and more sure it’s a good idea- maybe an important one too. Please indulge me while I passionately explain.
First, this article does a good job explaining the rot that currently exists at S&P. The system of credit ratings undermines the trust of even the most fervently pro-business entrepreneur out there. The models are knowingly games by both sides, and it’s clearly both corrupt and important. It’s also a bipartisan issue: Republicans and Democrats alike should want transparency when it comes to modeling downgrades- at the very least so they can argue against the results in a factual way. There’s no reason I can see why there shouldn’t be broad support for a rule to force the ratings agencies to make their models publicly available. In other words, this isn’t a political game that would score points for one side or the other.
Second, this article discusses why downgrades, interpreted as “default risk increases” on sovereign debt doesn’t really make sense- and uses as example Japan, which was downgraded in 2002 but still continues to have ridiculously low market-determined interest rates. In other words, ratings on governments, at least the ones that can print their own money (so not Greece), should be taken as a metaphor of their fiscal problems, or perhaps as a measurement of the risk that they will have potentially spiraling inflation when they do print their way out of a mess. An open source quantitative model would not directly try to model the failure of politicians to agree (although there are certainly market data proxies for that kind of indecision), and that’s ok: probably the quantitative model’s grade on sovereign default risk trained on corporate bonds would still give real information, even if it’s not default likelihood information. And, being open-source, it would at least be clear what it’s measuring and how.
I’ve also gotten a couple excellent comments already on my first post about this idea which I’d like to quickly address.
There’s a comment pointing out that it would take real resources to do this and to do it well: that’s for sure, but on the other hand it’s a hot topic right now and people may really want to sponsor it if they think it would be done well and widely adopted.
Another commenter had concerns of the potential for vandals to influence and game the model. But here’s the thing, the point of open source is that, although it’s impossible to avoid letting some people have more influence than others on the model (especially the maintainer), this risk is mitigated in two important ways. First of all it’s at least clear what is going on, which is way more than you can say for S&P, where there was outrageous gaming going on and nobody knew (or more correctly nobody did anything about it). Secondly, and more importantly, it’s always possible for someone to fork the open source model and start their own version if they think it’s become corrupt or too heavily influenced by certain methodologies or modeling choices. As they say, if you don’t like it, fork it.
Update! There’s a great article here about how the SEC is protecting the virtual ratings monopoly of S&P, Moody’s, and Fitch.
Open Source Ratings Model?
A couple of days ago I got this comment from a reader, which got me super excited.
His proposal is that we could start an open source ratings model to compete with S&P and Moody’s and Fitch ratings. I have made a few relevant lists which I want to share with you to address this idea.
Reasons to have an open source ratings model:
- The current rating agencies have a reputation for bad modeling; in particular, their models, upon examination, often have extremely unrealistic underlying assumptions. This could be rooted out and modified if a community of modelers and traders did their honest best to realistically model default.
- The current ratings agencies also have enormous power, as exemplified in the past few days of crazy volatile trading after S&P downgraded the debt of the U.S. (although the European debt problems are just as much to blame for that I believe). An alternative credit model, if it was well-known and trusted, would dilute their power.
- Although the rating agency shared descriptions of their models with their clients, they weren’t in fact open-source, and indeed the level of exchange probably served only to allow the clients to game the models. One of the goals of an open-source ratings model would be to avoid easy gaming.
- Just to show you how not open source S&P is currently, check out this article where they argue that they shouldn’t have to admit their mistakes. When you combine the power they wield, their reputation for sloppy reasoning, and their insistence on being protected from their mistakes, it is a pretty idiotic system.
- The ratings agencies also have a virtual lock on their industry- it is in fact incredibly difficult to open a new ratings agency, as I know from my experience at Riskmetrics, where we looked into doing so. By starting an open source ratings model, we can (hopefully) avoid issues like permits or whatever the problem was by not charging money and just listing free opinions.
Obstructions to starting an open source ratings model:
- It’s a lot of work, and we would need to set it up in some kind of wiki way so people could contribute to it. In fact it would have to me more Linux style, where some person or people maintain the model and the suggestions. Again, lots of work.
- Data! A good model requires lots of good data. Altman’s Z-score default model, which friends of mine worked on with him at Riskmetrics and then MSCI, could be the basis of an open source model, since it is being published. But the data that trains the model isn’t altogether publicly available. I’m working on this, would love to hear readers’ comments.
What is an open source model?
- The model itself is written in an open source language such as python or R and is publicly available for download.
- The data is also publicly available, and together with the above, this means people can download the data and model and change the parameters of the model to test for robustness- they can also change or tweak the model themselves.
- There is good documentation of the model describing how it was created.
- There is an account kept of how often different models are tried on the in-sample data. This prevents a kind of data fitting that people generally don’t think about enough, namely trying so many different models on one data set that eventually some model will look really good.
Data Viz
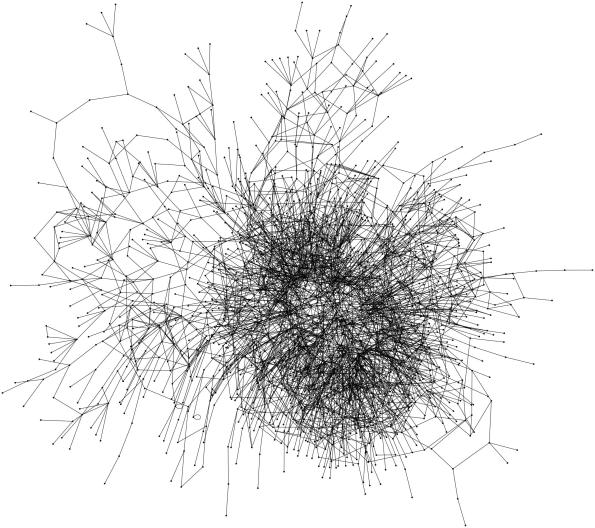
The picture below is a visualization of the complexity of algebra. The vertices are theorems and the edges between theorems are dependencies. Technically the edges should be directed, since if Theorem A depends on Theorem B, we shouldn’t have it the other way around too!
This comes from data mining my husband’s open source Stacks Project; I should admit that, even though I suggested the design of the picture, I didn’t implement it! My husband used graphviz to generate this picture – it puts heavily connected things in the middle and less connected things on the outside. I’ve also used graphviz to visualize the connections in databases (MySQL automatically generates the graph).
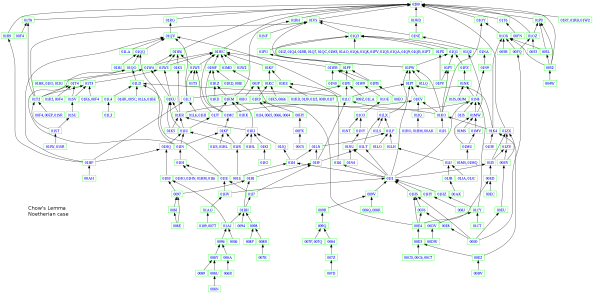
Here’s another picture which labels each vertex with a tag. I designed the tag system, which gives each theorem a unique identifier; the hope is that people will be willing to refer to the theorems in the project even though their names and theorem numbers may change (i.e. Theorem 1.3.3 may become Theorem 1.3.4 if someone adds a new result in that section). It’s also directed, showing you dependency (Theorem A points to Theorem B if you need Theorem A to prove Theorem B). This visualizes the results needed to prove Chow’s Lemma:
Some R code and a data mining book
I’m very pleased to add some R code which does essentially the same thing as my python code for this post, which was about using Bayesian inference to thing about women on boards of directors of S&P companies, and for this post, which was about measuring historical volatility for the S&P index. I have added the code to those respective posts. Hopefully the code will be useful for some of you to start practicing manipulating visualizing data in the two languages.
Thanks very much to Daniel Krasner for providing the R code!
Also, I wanted to mention a really good book I’m reading about data mining, namely “Data Analysis with Open Source Tools,” by Phillipp Janert, published by O’Reilly. He wrote it without assuming much mathematics, but in a sophisticated manner. In other words, for people who are mathematicians, the lack of explanation of the math will be fine, but the good news is he doesn’t dumb down the craft of modeling itself. And I like his approach, which is to never complicate stuff with fancy methods and tools unless you have a very clear grasp on what it will mean and why it’s going to improve the situation. In the end this is very similar to the book I would have imagined writing on data analysis, so I’m kind of annoyed that it’s already written and so good.
Speaking of O’Reilly, I’ll be at their “Strata: Making Data Work” conference next month here in New York, who’s going to meet me there? It looks pretty great, and will be a great chance to meet other people who are as in love with sexy data as I am.
Historical volatility on the S&P index
In a previous post I described the way people in finance often compute historical volatility, in order to try to anticipate future moves in a single stock. I’d like to give a couple of big caveats to this method as well as a worked example, namely on daily returns of the S&P index, with the accompanying python code. I will use these results in a future post I’m planning about errorbars and how people abuse and misuse them.
Two important characteristics of returns
First, market returns in general have fat-tailed distributions; things can seem “quiet” for long stretches of time (longer than any lookback window), during which the sample volatility is a possibly severe underestimate of the “true” standard of deviation of the underlying distribution (if that even makes sense – for the sake of this discussion let’s assume it does). Then when a fat-tailed event occurs, the sample volatility typically spikes to being an overestimate of the standard of deviation for that distribution.
Second, in the markets, there is clustering of volatility- another way of saying this is that volatility itself is rather auto-correlated, so even if we can’t predict the direction of the return, we can still estimate the size of the return. This is particularly true right after a shock, and there are time series models like ARCH and its cousins that model this phenomenon; they in fact allow you to model an overall auto-correlated volatility, which can be thought of as scaling for returns, and allows you to then approximate the normalized returns (returns divided by current volatility) as independent, although still not normal (because they are still fat-tailed even after removing the clustered volatility effect). See below for examples of normalized daily S&P returns with various decays.
Example: S&P daily returns
I got this data from Yahoo Finance, where they let you download daily S&P closes since 1950 to an excel spreadsheet. I could have used some other instrument class, but the below results would be stronger (especially for things like credit default swamps), not weaker- the S&P, being an index, is already the sum of a bunch of things and tends to be more normal as a result; in other words, the Central Limit Theorem is already taking effect on an intraday basis.
First let’s take a look at the last 3 years of closes, so starting in the summer of 2008:
Next we can look at the log returns for the past 3 years:
Now let’s look at how the historical volatility works out with different decays (decays are numbers less than 1 which you use to downweight old data: see this post for an explanation):
For each choice of the above decays, we can normalize the log returns. to try to remove the “volatility clustering”:
As we see, the long decay doesn’t do a very good job. In fact, here are the histograms, which are far from normal:
Here’s the python code I used to generate these plots from the data (see also R code below):
#!/usr/bin/env python
import csv
from matplotlib.pylab import *
from numpy import *
from math import *
import os
os.chdir(‘/Users/cathyoneil/python/sandp/’)
dataReader = csv.DictReader(open(‘SandP_data.txt’, ‘rU’), delimiter=’,’, quotechar=’|’)
close_list = []
for row in dataReader:
#print row[“Date”], row[“Close”]
close_list.append(float(row[“Close”]))
close_list.reverse()
close_array = array(close_list)
close_log_array = array([log(x) for x in close_list])
log_rets = array(diff(close_log_array))
perc_rets = array([exp(x)-1 for x in log_rets])
figure()
plot(close_array[-780:-1], label = “raw closes”)
title(“S&P closes for the last 3 years”)
legend(loc=2)
#figure()
#plot(log_rets, label = “log returns”)
#legend()
#figure()
#hist(log_rets, 100, label = “log returns”)
#legend()
#figure()
#hist(perc_rets, 100, label = “percentage returns”)
#legend()
#show()
def get_vol(d):
var = 0.0
lam = 0.0
var_list = []
for r in log_rets:
lam = lam*(1.0-1.0/d) + 1
var = (1-1.0/lam)*var + (1.0/lam)*r**2
var_list.append(var)
return [sqrt(x) for x in var_list]
figure()
for d in [10, 30, 100]:
plot(get_vol(d)[-780:-1], label = “decay factor %.2f” %(1-1.0/d))
title(“Volatility in the S&P in the past 3 years with different decay factors”)
legend()
for d in [10, 30, 100]:
figure()
these_vols = get_vol(d)
plot([log_rets[i]/these_vols[i-1] for i in range(len(log_rets) – 780, len(log_rets)-1)], label = “decay %.2f” %(1-1.0/d))
title(“Volatility normalized log returns (last three years)”)
legend()
figure()
plot([log_rets[i] for i in range(len(log_rets) – 780, len(log_rets)-1)], label = “raw log returns”)
title(“Raw log returns (last three years)”)
for d in [10, 30, 100]:
figure()
these_vols = get_vol(d)
normed_rets = [log_rets[i]/these_vols[i-1] for i in range(len(log_rets) – 780, len(log_rets)-1)]
hist(normed_rets, 100,label = “decay %.2f” %(1-1.0/d))
title(“Histogram of volatility normalized log returns (last three years)”)
legend()
Here’s the R code Daniel Krasner kindly wrote for the same plots:
setwd(“/Users/cathyoneil/R”)
dataReader <- read.csv(“SandP_data.txt”, header=T)
close_list <- as.numeric(dataReader$Close)
close_list <- rev(close_list)
close_log_list <- log(close_list)
log_rets <- diff(close_log_list)
perc_rets = exp(log_rets)-1
x11()
plot(close_list[(length(close_list)-779):(length(close_list))], type=’l’, main=”S&P closes for the last 3 years”, col=’blue’)
legend(125, 1300, “raw closes”, cex=0.8, col=”blue”, lty=1)
get_vol <- function(d){
var = 0
lam=0
var_list <- c()
for (r in log_rets){
lam <- lam*(1 – 1/d) + 1
var = (1 – 1/lam)*var + (1/lam)*r^2
var_list <- c(var_list, var)
}
return (sqrt(var_list))
}
L <- (length(close_list))
x11()
plot(get_vol(10)[(L-779):L], type=’l’, main=”Volatility in the S&P in the past 3 years with different decay factors”, col=1)
lines(get_vol(30)[(L-779):L], col=2)
lines(get_vol(100)[(L-779):L], col=3)
legend(550, 0.05, c(“decay factor .90”, “decay factor .97″,”decay factor .99”) , cex=0.8, col=c(1,2,3), lty = 1:3)
x11()
par(mfrow=c(3,1))
plot((log_rets[2:L]/get_vol(10))[(L-779):L], type=’l’, col=1, lty=1, ylab=”)
legend(620, 3, “decay factor .90”, cex=0.6, col=1, lty = 1)
plot((log_rets[2:L]/get_vol(30))[(L-779):L], type=’l’, col=2, lty =2, ylab=”)
legend(620, 3, “decay factor .97”, cex=0.6, col=2, lty = 2)
plot((log_rets[2:L]/get_vol(100))[(L-779):L], type=’l’, col=3, lty =3, ylab=”)
legend(620, 3, “decay factor .99”, cex=0.6, col=3, lty = 3)
x11()
plot(log_rets[(L-779):L], type=’l’, main = “raw log returns”, col=”blue”, ylab=”)
par(mfrow=c(3,1))
hist((log_rets[2:L]/get_vol(10))[(L-779):L], breaks=200, col=1, lty=1, ylab=”, xlab=”, main=”)
legend(2, 15, “decay factor .90”, cex=.8, col=1, lty = 1)
hist((log_rets[2:L]/get_vol(30))[(L-779):L], breaks=200, col=2, lty =2, ylab=”, xlab=”, main=”)
legend(2, 40, “decay factor .97”, cex=0.8, col=2, lty = 2)
hist((log_rets[2:L]/get_vol(100))[(L-779):L], breaks=200, col=3, lty =3, ylab=”, xlab=”, main=”)
legend(3, 50, “decay factor .99”, cex=0.8, col=3, lty = 3)
Glucose Prediction Model: absorption curves and dirty data
In this post I started visualizing some blood glucose data using python, and in this post my friend Daniel Krasner kindly rewrote my initial plots in R.
I am attempting to show how to follow the modeling techniques I discussed here in order to try to predict blood glucose levels. Although I listed a bunch of steps, I’m not going to be following them in exactly the order I wrote there, even though I tried to make them in more or less the order we should at least consider them.
For example, it says first to clean the data. However, until you decide a bit about what your model will be attempting to do, you don’t even know what dirty data really means or how to clean it. On the other hand, you don’t want to wait too long to figure something out about cleaning data. It’s kind of a craft rather than a science. I’m hoping that by explaining the steps the craft will become apparent. I’ll talk more about cleaning the data below.
Next, I suggested you choose in-sample and out-of-sample data sets. In this case I will use all of my data for my in-sample data since I happen to know it’s from last year (actually last spring) so I can always ask my friend to send me more recent data when my model is ready for testing. In general it’s a good idea to use at most two thirds of your data as in-sample; otherwise your out-of-sample test is not sufficiently meaningful (assuming you don’t have that much data, which always seems to be the case).
Next, I want to choose my predictive variables. First, we should try to see how much mileage we can get out of predicting future blood glucose levels with past glucose levels. Keeping in mind that the previous post had us using log levels instead of actual glucose levels, since then the distribution of levels is more normal, we will actually be trying to predict log glucose levels (log levels) knowing past log glucose levels.
One good stare at the data will tell us there’s probably more than one past data point that will be needed, since we see that there is pretty consistent moves upwards and downwards. In other words, there is autocorrelation in the log levels, which is to be expected, but we will want to look at the derivative of the log levels in the near past to predict the future log levels. The derivative can be computed by taking the difference of the most recent log level and the previous one to that.
Once we have the best model we can with just knowing past log levels, we will want to add reasonable other signals. The most obvious candidates are the insulin intakes and the carb intakes. These are presented as integer values with certain timestamps. Focusing on the insulin for now, if we know when the insulin is taken and how much, we should be able to model how much insulin has been absorbed into the blood stream at any given time, if we know what the insulin absorption curve looks like.
This leads to the question of, what does the insulin (rate of) absorption curve look like? I’ve heard that it’s pretty much bell-shaped, with a maximum at 1.5 hours from the time of intake; so it looks more or less like a normal distribution’s probability density function. It remains to guess what the maximum height should be, but it very likely depends linearly on the amount of insulin that was taken. We also need to guess at the standard deviation, although we have a pretty good head start knowing the 1.5 hours clue.
Next, the carb intakes will be similar to the insulin intake but trickier, since there is more than one type of carb and different types get absorbed at different rates, but are all absorbed by the bloodstream in a vaguely similar way, which is to say like a bell curve. We will have to be pretty careful to add the carb intake model, since probably the overall model will depend dramatically on our choices.
I’m getting ahead of myself, which is actually kind of good, because we want to make sure our hopeful path is somewhat clear and not too congested with unknowns. But let’s get back to the first step of modeling, which is just using past log glucose levels to predict the next glucose level (we will later try to expand the horizon of the model to predict glucose levels an hour from now).
Looking back at the data, we see gaps and we see crazy values sometimes. Moreover, we see crazy values more often near the gaps. This is probably due to the monitor crapping out near the end of its life and also near the beginning. Actually the weird values at the beginning are easy to take care of- since we are going to work causally, we will know there had been a gap and the data just restarted, so we we will know to ignore the values for a while (we will determine how long shortly) until we can trust the numbers. But it’s much trickier to deal with crazy values near the end of the monitor’s life, since, working causally, we won’t be able to look into the future and see that the monitor will die soon. This is a pretty serious dirty data problem, and the regression we plan to run may be overly affected by the crazy crapping-out monitor problems if we don’t figure out how to weed them out.
There are two things that may help. First, the monitor also has a data feed which is trying to measure the health of the monitor itself. If this monitor monitor is good, it may be exactly what we need to decide, “uh-oh the monitor is dying, stop trusting the data.” The second possible saving grace is that my friend also measured his blood glucose levels manually and inputted those numbers into the machine, which means we have a way to check the two sets of numbers against each other. Unfortunately he didn’t do this every five minutes (well actually that’s a good thing for him), and in particular during the night there were long gaps of time when we don’t have any manual measurements.
A final thought on modeling. We’ve mentioned three sources of signals, namely past blood glucose levels, insulin absorption forecasts, and carbohydrate absorption forecasts. There are a couple of other variables that are known to effect the blood glucose levels. Namely, the time of day and the amount of exercise that the person is doing. We won’t have access to exercise, but we do have access to timestamps. So it’s possible we can incorporate that data into the model as well, once we have some idea of how the glucose is effected by the time of day.
Women on a board of directors: let’s use Bayesian inference
I wanted to show how to perform a “women on the board of directors” analysis using Bayesian inference. What this means is that we need to form a “prior” on what we think the distribution of the answer could be, and then we update our prior with the data available. In this case we simplify the question we are trying to answer: given that we see a board with 3 women and 7 men (so 10 total), what is the fraction of women available for the board of directors in the general population? The reason we may want to answer this question is that then we can compare the answer to other available answers, derived other ways (say by looking at the makeup of upper level management) and see if there’s a bias.
In order to illustrate Bayesian techniques, I’ve simplified it further to be a discrete question. So I’ve pretended that there are only 11 answers you could possible have, namely that the fraction of available women (in the population of people qualified to be put on the board of directors) is 0%, 10%, 20%, …, 90%, or 100%.
Moreover, I’ve put the least judgmental prior on the situation, namely that there is an equal chance for any of these 11 possibilities. Thus the prior distribution is uniform:
The next step is to update our prior with the available data. In this case we have the data point that there a board with 3 women and 7 men. In this case we are sure that there are some women and some men available, so the updated probability of there being 0% women or 100% women should both be zero (and we will see that this is true). Moreover, we would expect to see that the most likely fraction will be 30%, and we will see that too. What Bayesian inference gives to us, though, is the relative probabilities of the other possibilities, based on the likelihood that one of them is true given the data. So for example if we are assuming for the moment that 70% of the qualified people are women, what is the likelihood that the board ends up being 3 women and 7 men? We can compute that as (0.70)^3*(0.30)^7. We multiply that by 1/11, the probability that 70% is the right answer (according to our prior) to get the “unscaled posterior distribution”, or the likelihoods of each possibility. Here’s a graph of these numbers when I do it for all 11 possibilities:
In order to make this a probability distribution we need to make sure the total adds up to 1, so we scale to get the actual posterior distribution:
What we observe is, for example, that it’s about twice as likely for 50% of women to be qualified as it is for 10% of women to be qualified, even though those answers are equally distant from the best guess of 30%. This kind of “confidence of error” is what Bayesian inference is good for. Also, keep in mind that if we had had a more informed prior the above graph would look different; for example we could use the above graph as a prior for the next time we come across a board of directors. In fact that’s exactly how this kind of inference is used: iteratively, as we travel forward through time collecting data. We typically want to start out with a prior that is pretty mild (like the uniform distribution above) so that we aren’t skewing the end results too much, and let the data speak for itself. In fact priors are typically of the form, “things should vary smoothly”; more on what that could possibly mean in a later post.
Here’s the python code I wrote to make these graphs:
Here’s the R code that Daniel Krasner wrote for these graphs:
Woohoo!
First of all, I changed the theme of the blog, because I am getting really excellent comments from people but I thought it was too difficult to read the comments and to leave comments with the old theme. This way you can just click on the word “Go to comments” or “Leave a comment” which is a bit more self-evident to design-ignorant people like me. Hope you like it.
Next, I had a bad day today, but I’m very happy to report that something has raised my spirits. Namely, Jake Porway from Data Without Borders and I have been corresponding, and I’ve offered to talk to prospective NGO’s about data, what they should be collecting depending on what kind of studies they want to be able to perform, and how to store and revise data. It looks like it’s really going to happen!
In fact his exact words were: I will definitely reach out to you when we’re talking to NPOs / NGOs.
Oh, and by the way, he also says I can blog about our conversations together as well as my future conversations with those NGO’s (as long as they’re cool with it), which will be super interesting.
Oh, yeah. Can I get a WOOHOO?!?
Step 0 Revisited: Doing it in R
A nerd friend of mine kindly rewrote my python scripts in R and produced similar looking graphs. I downloaded R from here and one thing that’s cool is that once it’s installed, if you open an R source code (ending with “.R”), an R console pops up automatically and you can just start working. Here’s the code:
gdata <- read.csv('large_data_glucose.csv', header=TRUE)
#We can open a spreadsheet type editor to check out and edit the data: edit(gdata) #Since we are interested in the glucose sensor data, column 31, but the name is a bit awkward to deal with, a good thing to do is to change it: colnames(gdata)[31] <- "GSensor" #Lets plot the glucose sensor data: plot(gdata$GSensor, col="darkblue") #Here's a histogram plot: hist(gdata$GSensor, breaks=100, col="darkblue")
#and now lets plot the logarithm of the data: hist(log(gdata$GSensor), breaks=100, col="darkblue")
And here are the plots:
One thing my friend mentions is that R automatically skips missing values (whereas we had to deal with them directly in python). He also mentions that other things can be done in this situation, and to learn more we should check out this site.
R seems to be really good at this kind of thing, that is to say doing the first thing you can think about with data. I am wondering how it compares to python when you have to really start cleaning and processing the data before plotting. We shall see!
Step 0: Installing python and visualizing data
A friend of mine has type I diabetes, and lots of data (glucose levels every five minutes) from his monitor. We’ve talked on and off about how to model future (as in one hour hence) glucose levels, using information on the current level, insulin intake, and carb intake. He was kind enough to allow me to work on this project on this blog. It’s an exciting and potentially really useful project, and it will be great to use as an example for each step of the modeling process.
To be clear: I don’t know if I will be able to successfully model glucose levels (or even better be able to make suggestions for how much insulin or carbs to take in order to keep glucose levels within reasonable levels), but it’s exciting to try and it’s totally worth a try. I’m counting on you to give me suggestions if I’m being dumb and missing something!
I decided to use python to do my modeling, and I went to this awesomely useful page and followed the instructions to install python and matplotlib on my oldish mac book. It worked perfectly (thanks, nerd who wrote that page!).
The data file, which contains 3 months of data, is a csv (comma separated values) file, with the first line describing the name of the values in the lines below it:
Index,Date,Time,Timestamp,New Device Time,BG Reading (mg/dL),Linked BG Meter ID,Temp Basal Amount (U/h),Temp Basal Type,Temp Basal Duration (hh:mm:ss),Bolus Type,Bolus Volume Selected (U),Bolus Volume Delive\ red (U),Programmed Bolus Duration (hh:mm:ss),Prime Type,Prime Volume Delivered (U),Suspend,Rewind,BWZ Estimate (U),BWZ Target High BG (mg/dL),BWZ Target Low BG (mg/dL),BWZ Carb Ratio (grams),BWZ Insulin Sens\ itivity (mg/dL),BWZ Carb Input (grams),BWZ BG Input (mg/dL),BWZ Correction Estimate (U),BWZ Food Estimate (U),BWZ Active Insulin (U),Alarm,Sensor Calibration BG (mg/dL),Sensor Glucose (mg/dL),ISIG Value,Dail\ y Insulin Total (U),Raw-Type,Raw-Values,Raw-ID,Raw-Upload ID,Raw-Seq Num,Raw-Device Type 1,12/15/10,00:00:00,12/15/10 00:00:00,,,,,,,,,,,,,,,,,,,,,,,,,,,,,28.4,ResultDailyTotal,"AMOUNT=28.4, CONCENTRATION=null",5472682886,50184670,236,Paradigm 522 2,12/15/10,00:04:00,12/15/10 00:04:00,,,,,,,,,,,,,,,,,,,,,,,,,,,120,16.54,,GlucoseSensorData,"AMOUNT=120, ISIG=16.54, VCNTR=null, BACKFILL_INDICATOR=null",5472689886,50184670,4240,Paradigm 522 3,12/15/10,00:09:00,12/15/10 00:09:00,,,,,,,,,,,,,,,,,,,,,,,,,,,116,16.21,,GlucoseSensorData,"AMOUNT=116, ISIG=16.21, VCNTR=null, BACKFILL_INDICATOR=null",5472689885,50184670,4239,Paradigm 522
I made a new directory below my home directory for this file and for the python scripts to live, and I started up python from the command line inside that directory. Then I opened emacs (could have been TextEdit or any other editor you like) to write simple script to see my data.
A really easy way of importing this kind of file into python is to use a DictReader. DictReader is looking for a file formatted exactly as this file is, and it’s easy to use. I wrote this simple script to take a look at the values in the “Sensor Glucose” field (note there are sometimes gaps and I had to decide what to do in that case):
And this is the picture that popped out:
I don’t know how easy it is to see this but there are lots of gaps (when there’s a gap I plotted a dot at -1, and the line at -1 looks pretty thick). Moreover, it’s clear this data is being kept in a pretty tight range (probably good news for my friend). Another thing you might notice is that the data looks more likely to be in the lower half of the range than in the upper half. To get at this we will draw a histogram of the data, but this time we will *not* fill in gaps with a bunch of fake “-1″s since that would throw off the histogram. Here are the lines I added in the code:
And this is the histogram that resulted:
This is a pretty skewed, pretty long right-tailed distribution. Since we know the data is always positive (it’s measuring the presence of something in the blood stream), and since the distribution is skewed, this makes me consider using the log values instead of the actual values. This is because, as a rule of thumb, it’s better to use variables that are more or less normally distributed. To picture this I replace one line in my code:
skip_gaps_datalist.append(log(float(row["Sensor Glucose (mg/dL)"])))
And this is the new histogram:
This is definitely more normal.
Next time we will talk more about cleaning this data and what other data we will use for the model.