Forecasting precipitation
What does it means when you’re given a precipitation forecast? And how do you know if it’s accurate? What does it mean when you see that there’s a 37% chance of rain?
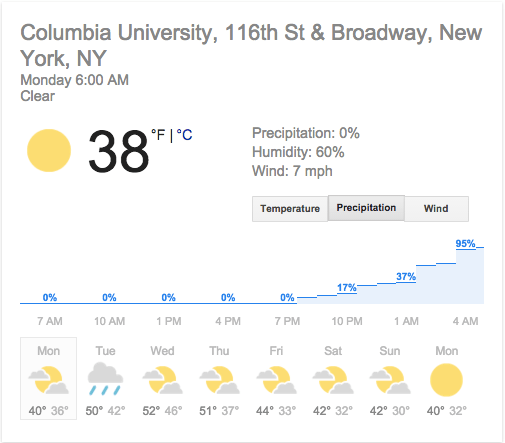
Well, there are two input variables you have to keep in mind: first, the geographic location – where you’re looking for a forecast, and second, the time window you’re looking at.
For simplicity let’s fix a specific spot – say 116th and Broadway – and let’s also fix a specific one hour time window, say 1am-2am.
Now we can ask again, how would we interpret a “37% chance of rain” for this location during this time? And when do we decide our forecast is good? It’s trickier than you might think.
***
Let’s first think about interpretation. Hopefully what that phrase means is something like, 37 out of 100 times, with these exact conditions, you’ll see a non-zero, measurable amount of rain or other precipitation during an hour. So far so good.
Of course, we only have exactly one of these exact hours. So we cannot directly test the forecast with that one hour. Instead, we should collect a lot of data on the forecast. Start by building 101 bins, labeled from 0 to 100, and throw each forecasted hour into the appropriate bin, along with a record of the actual precipitation outcome.
So if it actually rains between 1am and 2am at 116th and Columbia, I’d throw this record into the “37” bin, along with a note that said “YES IT RAINED.” I’d short hand this note by attaching a “1” to the record, which stands for “100% chance of rain because it actually rained.” I’d attach a “0” to each hour where it didn’t rain.
I’d do this for every single hour of every single day and at every single location as well, of course not into the “37” bin but into the bin with the forecasted number, along with the note of whether rain came. I’d do this for 100 years, or at least 1, and by the end of it I’d presumably have a lot of data in each bin.
So for the “0” bin I’d have many many hours where there wasn’t supposed to be rain. Was there sometimes rain? Yeah, probably. So my “0” bin would have a bunch of records with “0” labels and a few with “1” labels. Each time a “1” record made its way into the “0” bin, it would represent a failure of the model. I’d need to count such a failure against the model somehow.
But then again, what about the “37” bin? Well I’d want to know, for all the hours forecasted to have a 37% chance of rain, how often it actually happened. If I ended up with 100 examples, I’d hope that 37 our of the 100 examples ended up with rain. If it actually happened 50 times out of 100, I’d be disappointed – another failure of the model. I’d need to count this against the model.
Of course to be more careful I’d rather have 100,000 examples accumulated in bin “37” and see 50,000 of those hours actually had rain. With that data I’d be fairly certain this forecasting engine is inaccurate.
Or, if 37,003 of those examples actually saw rain, then I’d be extremely pleased. I’d be happy to trust this model when it says 37% chance of rain. But then again, it might still be kind of inaccurate when it comes to the bin labeled “72”.
We’ve worked so hard to interpret the forecast that we’re pretty close to determining if it’s accurate. Let’s go ahead and finish the job.
***
Let’s take a quick reality check first though. Since I’ve already decided to fix on a specific location, namely at 116th and Broadway, the ideal forecast would always just be 1 or 0: it’s either going to rain or it’s not.
In other words, we have the ideal forecast to measure all other forecasts against. Let’s call that God’s forecast, or if you’re an atheist like me, call it “mother nature’s forecast,” or MNF for short. If you tried to test MNF, you’d set up your 101 bins but you’d only ever use 2 of them. And they’d always be right.
***
OK, but this is the real world, and forecasting weather is hard, especially when it’s a day or two in advance, so let’s try instead to compare two forecasts head to head. Which one is better, Google or Dark Sky?
I’d want a way to assign scores to each of them and choose the better precipitation model. Here’s how I’d do it.
First, I’d do the bin thing for each of them, over the same time period. Let’s say I’m still obsessed with my spot, 116th and Broadway, and I’ve fixed a year or two of hourly forecasts to compare the two models.
Here’s my method. Instead of rewarding a model for accuracy, I’m going to penalize it for inaccuracy. Specifically, I’ll assign it a squared error term for each time it forecast wrong.
To see how that plays out, let’s look at the “37” bin for each model. As we mentioned above, any time the model forecasts 37% chance of rain, it’s wrong. It either rains, in which case it’s off by 1.00-0.37 = 0.63, or it doesn’t rain, in which case the error term is 0.37. I will assign it the square of those terms as penalty for its wrongness.
***
How did I come up with the square of the error term? Why is it a good choice? For one, it has the following magical property: it will be minimized when the label “37” is the most accurate.
In other words, if we fix for a moment the records that end up in the “37” bin, the sum of the squared error terms will be the smallest when the true proportion of “1”s to “0”s in that bin is 37%.
Said another way, if we have 100,000 records in the “37” bin, and actually 50,000 of them correspond to rainy hours, then the sum of all the squared error terms ends up much bigger than if only 37,000 of them turned into rain. So that’s a way of penalizing a model for inaccuracy.
To be more precise, if our true chances of rain is but our bin is actually labeled
then the average penalty term, assuming we’ve collected enough data to ignore measurement error, will be
or
The crucial fact is that is always positive, so the above penalty term will be minimized when
is zero, or in other words when the label of the bin perfectly corresponds to the actual chance of rain.
Moreover, other ways of penalizing a specific record in the “37” bin, say by summing up the absolute value of the error term, don’t have this property.
***
The above has nothing to do with “bin 37,” of course. I could have chosen any bin. To compare two forecasting models, then, we add up all the squared error terms of all the forecasts over a fixed time period.
Note that any model that ever spits out “37” is going to get some error no matter what. Or in other words, a model that wants to be closer to MNF would minimize the number of forecasts to put into the “37” bin and try hard to put forecasts into either the “0” bin or the “1” bin, assuming of course that they had confidence in the forecast.
Actually, the worst of all bins – the one the forecast accumulates the most penalty for – is the “50” bin. Putting an hourly forecast into the “50” bin is like giving up – you’re going to get a big penalty no matter what, because again, it’s either going to rain or it isn’t. Said another way, the above error term is maximized at
.
But the beauty of the square error penalty is that it also rewards certainty. Another way of saying this is that, if I am a forecast and I want to improve my score, I can either:
- make sure the forecasts in each bin are as accurate as possible, or
- try to get some of the forecasts in each bin out of their current bins and closer to either 0 or 1.
Either way their total sum of square error will go down.
I’m dwelling on this because there’s a forecast out there that we want to make sure is deeply shamed by any self-respecting scoring system. Namely, the forecast that says there’s a n% chance of rain for every hour of every day, where n is chosen to be the average hourly chance of rain. This is a super dumb forecast, and we want to make sure it doesn’t score as well as God or mother nature, and thankfully it doesn’t (even though it’s perfectly accurate within each bin, and it only uses one bin).
Then again, it would be good to make sure Google scores better than the super dumb forecast, which I’d be happy to do if I could actually get my hands on this data.
***
One last thing. This entire conversation assumed that the geographic location is fixed at 116th and Broadway. In general, forecasts are made over some larger land mass, and that fact affects the precipitation forecast. Specifically, if there’s an 80% chance that precipitation will occur over half the land mass and a 0% chance it will occur over the other half for a specific time window, the forecast will read 40%. This is something like the chance that an average person in that land mass will experience precipitation, assuming they don’t move and that people are equidistributed over the land mass.
Then again with the proliferation of apps that intend to give forecasts for pinpointed locations, this old-fashioned forecasting method will probably be gone soon.



There is some interesting theory related to coming up with well-calibrated forecasts. In particular, it is possible to come up with asymptotically well-calibrated forecasts even if the weather each day is determined by an adversarial god, bent on making the forecaster look bad (so actual knowledge of the weather doesn’t help the weatherman according to this metric, in the limit): http://gosset.wharton.upenn.edu/research/calibration.pdf
LikeLiked by 1 person
If you want to compare two punctilistic forecasts, say, 37% vs. 23%, Bayesian updating is non-controversial. You do not have to worry about a prior distribution over the whole range of possibilities. Just assign an equal prior weight to each forecast. 🙂
LikeLike
Shouldn’t that be $t(1-t) + \epsilon^2$
(without the factor of two, and with the sign reversed)
LikeLike
Well it’s true I lost the scrap paper where I did this calculation. It started as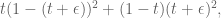 that’s what I remember. And yeah I’m sure you’re right. Thanks, I’ll correct it.
that’s what I remember. And yeah I’m sure you’re right. Thanks, I’ll correct it.
LikeLike
Aside from squared error, it looks like Wikipedia (https://en.wikipedia.org/wiki/Scoring_rule) lists two other proper scoring rules (though given that weather predictions occasionally assign zero probabilities to events that end up happening, I suppose that logarithmic scoring isn’t suitable here).
On the other hand, it’s not clear that a proper scoring rule necessarily makes sense here: maybe we really want a loss function that penalizes them more for predicting a low probability of rain when it rains than vice versa. I wonder what the loss function looks like for people deciding whether to close schools based on snow predictions…
LikeLike
Yeah I was thinking about this too, although it seemed a bit far afield for the post. Like, what if I don’t care about the difference between 75% or 100%, because in either case I’m taking an umbrella? Could I get a tailored app to work for me especially well if I tell it what to care about?
LikeLike
The “locality” property of the logarithmic scoring rule (see the above-linked wikipedia page) is, IMO, a pretty nice property, albeit irrelevant for binary questions like “will it it rain?”. Since the logarithmic scoring rule is essentially the only proper scoring rule that has this property (up to affine transformations), it’s in some sense “canonical”, so philosophically I think you need a really good argument to use any other loss function. Being able to quantify your actual utility function (e.g. in terms of whether you’ll carry an umbrella and how much of a pain that is) could perhaps be a really good argument. But since weather forecasts are prepared for a vast, heterogeneous audience with a variety of utility functions, going with the canonical loss still might be a good idea.
Another perspective on the logarithmic scoring rule can be obtained by thinking about it in a prediction market context. (See http://mason.gmu.edu/~rhanson/mktscore.pdf.) In this context, logarithmic scoring rule has a natural interpretation in terms of relative entropy (KL-divergence). This interpretation can be generalized to other families of scoring rules (http://www.sipta.org/isipta07/proceedings/papers/s076.pdf) but I don’t believe the quadratic scoring rule is particularly natural in this framework.
Phil Tetlock is probably the world’s leading expert on forecasting, and he tends to use the Brier (quadratic loss) scoring rule in his research. (BTW I recommend his book Superforecasting if you’re interested in this subject.) A friend of mine who works for Cultivate Labs, a prediction market software platform company, also likes the Brier score. I think their intuition is that the logarithmic scoring rule’s infinite penalty for forecasting 0% probability for an event that actually takes place, is inconsistent with how human beings actually make and consume forecasts. You want to penalize people for this mistake, but not bankrupt them permanently.
LikeLike
ICYMI The Signal and the Noise: Why So Many Predictions Fail-but Some Don’t
by Nate Silver has a discussion of how the predictions of rain from NOAA are increased by TV weather reporters because people get angrier when no rain is forecasted and they get wet than the opposite. What Makes a Forecast Good? (p. 128)
LikeLike
“Wet bias”!
LikeLike
mathbabe is sexy:
r-prediction = 0.01
LikeLike
Cathy, the word you’re looking for is “demiurge”, see http://www.m-w.com:
Definition of demiurge
1 capitalized a : a Platonic subordinate deity who fashions the sensible world in the light of eternal ideas b : a Gnostic subordinate deity who is the creator of the material world
2: one that is an autonomous creative force or decisive power
LikeLike
Thank you so much for this!
I think the following is a bit misleading:
>In other words, if we fix for a moment the records that end up in the “37” bin, the sum of the squared error terms will be the smallest when the true proportion of “1”s to “0”s in that bin is 37%.
> Said another way, if we have 100,000 records in the “37” bin, and actually 50,000 of them correspond to rainy hours, then the sum of all the squared error terms ends up much bigger than if only 37,000 of them turned into rain.
If you fix the _number_ of records that end up in the 37 bin, you fix the label, but you can vary the 1’s and 0’s, (which is how the above reads), then the error is minimized when all the records are 0’s, since each of them adds 0.37^2 to the total error, which is less than (1-0.37)^2.
I guess you meant that the rainfall is fixed, but which bin we put that collection of records in is not. But I found it confusing.
LikeLike
I don’t understand why the error term should be minimal if the prediction was accurate. The penalty for no rain (0.37^2) is smaller than the penalty for rain (0.63)^2, so the minimum of the error term actually occurs when it never rains.
Shouldn’t you rather just subtract the predicted fraction from the observed fraction in each bin, divide the difference by the Poisson noise for that bin, and sum up the squares of all those differences?
LikeLike
Interesting. I never thought very much about weather prediction.
Having lived in both very rainy places and places with droughts (basically, the degenerate cases for prediction), I’m less interested in whether it will rain and more interested in expected rainfall, heaviness of rainfall, and the duration of rain (as in, don’t bother telling me about 30 second squalls). I’ve yet to find anything better than either radar maps or looking out the window. Are there any sites that attempt these sorts of predictions?
LikeLike
Good summary, and commenters got some of the finer points.
A mathematically significant difference is the actual process used. The error analysis is performed on the forecasting system as a whole, not just for a particular location. A typical model will make forecasts for thousands of locations, at dozens of elevations, for dozens of forecast times. This is done every six hours typically, and results in a sufficiently massive data set that you can do interesting and valid statistical analysis. These data points will have decaying non-linear correlations in time and space, so it’s not simple. The analysis is also used to gain understanding of the quality and improve the simulation of the real world physics. So it’s not strictly a minimum error of the specific forecast that yields 37%. It’s a simulation with total system managed error that yields a specific forecast of 37%.
The statistics of the errors is also used to compute “skill”. This is occasionally made public in special situations. You may have a forecast of 37% with a very large residual errror estimate or with a very small error estimate. The residual errors indicate “skill” using various more subtle statistical methods.
The most common public discussion of “skill” is around hurricanes. All of the different hurricane models show good skill in predicting the track of the center a hurricane, but have low skill in predicting the size or strength of a hurricane. The forecasters try a variety of ways to convey that the difference. This matters to the public because the impact of a small weak hurricane centered 50 miles away is completely different than that of a large powerful hurricane 50 miles away.
The current next level is to separate modeling skill from initial measurement uncertainty with ensemble modeling. In one dimension there are a variety of different physical simulations with names like GFS, NAM, ECMWF, etc. Human and automatic forecasters will compare their results and their skill characteristics to adjust local forecasts. They may also make vague statements about uncertainty (beyond the 37%) when there is substantial differences. Substantial differences can indicate a low skill situation.
In the other dimension the same model will be run many times using different initial noise additions to the observed data. The resulting variation is an indication of the internal components of error. Some of the error is from differences between the real world and the simulated physics. Some of the error is from differences between the measurements and the real world. You cannot measure the characteristics of a block of air many miles on each side perfectly. There are always errors.
Ensemble modeling tools are now available in production, but there is a lot to be learned.
LikeLike