If it’s hocus pocus then it’s not math
A few days ago there was a kerfuffle over this “numberphile” video, which was blogged about in Slate here by Phil Plait in his “Bad Astronomy” column, with a followup post here with an apology and a great quote from my friend Jordan Ellenberg.
The original video is hideous and should never have gotten attention in the first place. I say that not because the subject couldn’t have been done well – it could have, for sure – but because it was done so poorly that it ends up being destructive to the public’s most basic understanding of math and in particular positive versus negative numbers. My least favorite line from the crappy video:
I was trying to come up with an intuitive reason for this I and I just couldn’t. You have to do the mathematical hocus pocus to see it.
What??
Anything that is hocus pocus isn’t actually math. And people who don’t understand that shouldn’t be making math videos for public consumption, especially ones that have MSRI’s logo on them and get written up in Slate. Yuck!
I’m not going to just vent about the cultural context, though, I’m going to mention what the actual mathematical object of study was in this video. Namely, it’s an argument that “prove” that we have the following identity:
Wait, how can that be? Isn’t the left hand side positive and the right hand side negative?!
This mathematical argument is familiar to me – in fact it is very much along the lines of stuff we sometimes cover at the math summer program HCSSiM I teach at sometimes (see my notes from 2012 here). But in the case of HCSSiM, we do it quite differently. Specifically, we use it as a demonstration of flawed mathematical thinking. Then we take note and make sure we’re more careful in the future.
If you watch the video, you will see the flaw almost immediately. Namely, it starts with the question of what the value is of the infinite sum
But here’s the thing, that doesn’t actually have a value. That is, it doesn’t have a value until you assign it a value, which you can do but then you might want to absolutely positively must explain how you’ve done so. Instead of that explanation, the guy in the video just acts like it’s obvious and uses that “fact,” along with a bunch of super careless moving around of terms in infinite sums, to infer the above outrageous identity.
To be clear, sometimes infinite sums do have pretty intuitive and reasonable values (even though you should be careful to acknowledge that they too are assigned rather than “true”). For example, any geometric series where each successive term gets smaller has an actual “converging sum”. The most canonical example of this is the following:
What’s nice about this sum is that it is naively plausible. Our intuition from elementary school is corroborated when we think about eating half a cake, then another quarter, and then half of what’s left, and so on, and it makes sense to us that, if we did that forever (or if we did that increasingly quickly) we’d end up eating the whole cake.
This concept has a name, and it’s convergence, and it jibes with our sense of what would happen “if we kept doing stuff forever (again at possibly increasing speed).” The amounts we’ve measured on the way to forever are called partial sums, and we make sure they converge to the answer. In the example above the partial sums are and so on, and they definitely converge to 1.
There’s a mathematical way of defining convergence of series like this that the geometric series follows but that the series does not. Namely, you guess the answer, and to make sure you’ve got the right one, you make sure that all of the partial sums are very very close to that answer if you go far enough, for any definition of “very very close.”
So if you want it to get within 0.00001, there’s a number N so that, after the Nth partial sum, all partial sums are within 0.00001 of the answer. And so on.
Notice that if you take the partial sums of the series you get the sequence
which doesn’t get closer and closer to anything. That’s another way of saying that there is no naively plausible value for this infinite sum.
As for the first infinite sum we came across, the that does have a naively plausible value, which we call “infinity.” Totally cool and satisfying to your intuition that you worked so hard to achieve in high school.
But here’s the thing. Mathematicians are pretty clever, so they haven’t stopped there, and they’ve assigned a value to the infinite sum in spite of these pesky intuition issues, namely
, and in a weird mathematical universe of their construction, which is wildly useful in some contexts, that value is internally consistent with other crazy-ass things. One of those other crazy-ass things is the original identity
[Note: what would be really cool is if a mathematician made a video explaining the crazy-ass universe and why it’s useful and in what contexts. This might be hard and it’s not my expertise but I for one would love to watch that video.]
That doesn’t mean the identity is “true” in any intuitively plausible sense of the word. It means that mathematicians are scrappy.
Now here’s my last point, and it’s the only place I disagree somewhat (I think) with Jordan in his tweets. Namely, I really do think that the intuitive definition is qualitatively different from what I’ve termed the “crazy-ass” definition. Maybe not in a context where you’re talking to other mathematicians, and everyone is sufficiently sophisticated to know what’s going on, but definitely in the context of explaining math to the public where you can rely on number sense and (hopefully!) a strong intuition that positive numbers can’t suddenly become negative numbers.
Specifically, if you can’t make any sense of it, intuitive or otherwise, and if you have to ascribe it to “mathematical hocus pocus,” then you’re definitely doing something wrong. Please stop.



Infinity is weirder than most of us can imagine. The thing that gets me is – why is the infinite sum diddling invalid, while the Hilbert’s Hotel proof is sound?
LikeLike
I think the problem isn’t that one _result_ is valid and one is invalid, it’s that the _argument_ in the video is totally bogus.
Yes, infinity as a concept is weird and difficult to wrap our heads around. But a priori, all you need to understand about the infinite hotel is that, for any natural number you pick, there’s a room with that number. Then, if I have two full hotels (call them Y and P) and want to reassign the rooms so it’s only one hotel, then I can give you an explicit formula so that you know exactly where the occupants of room 17 Y will be placed, as well as which stop of the process this will happen. Then we will use Cathy’s “intuition” about eating cake and say we’ll do each assignment in half as much time as the one before (perhaps via teleporters, whatever). This is “sound,” as you put it, because to a nonmathematician it still uses some shred of the real world (modulo teleporters) – specifically, numbers. The occupants of room 17Y will get put in room 34P, and if you ask me about the occupants of any other room, I can give you an explicit number (people in hotel Y get put in room 2x, and people in hotel P get put in room 2x – 1). The only leap is the 1 + 1/2 + 1/4… bit for how we can do this in a reasonable amount of time, but again – since we have instant teleportation, it makes sense that we can get someone into the correct room within 1/2^100 of a second.
The video, on the other hand, starts by saying “1 – 1 + 1 -1 + 1 … = 1/2″ without giving any justification whatsoever. They simply claim it as fact – and that’s the bad mathematics right there. They offer no explanation that this is a trick they are using to make sense of an otherwise nonsensical thing. In particular, they are taking something that we have explicitly good arguments for (1 -1 + 1… does not converge under the epsilon-N model) and ignoring the fact that they are actually just defining that series rather than actually showing the mathematics that leads to that conclusion (that it’s 1/2).
So, in summary: The infinite sum diddling if invalid because they don’t do anything to validate it. It _can_ be valid, but that would require giving some context.
LikeLike
Does an infinite sum have only one meaning, viz. its sequence of partial sums?
LikeLike
the big jump is 1-1+1-1+1…= 1/2, after that it is pretty basic, so I really don’t get your criticism regarding “super careless moving” around of terms. As far I can see it is just the associative property of addition (for me 5th grade math), the next steps are algebra (9th grade), but nothing that is esoteric or difficult. He could have explained the first sum better (but given the video length I doubt he could). I sent the video to my son on friday, and it set him off trying to figure out the first step, which was good.
LikeLike
The associative property works for finite numbers of addends, but you can’t necessarily do it for an infinite number of terms. Even with some convergent series (called conditionally convergent), you will get different answers if you rearrange the terms. (For more info, try this: http://en.wikipedia.org/wiki/Riemann_series_theorem.)
LikeLike
Thanks for posting this. I saw it on facebook four days ago and it made me angry. I even thought about asking you about it.
LikeLike
Cool, me too. Feel free to send me links though.
LikeLike
Thank you!!! I’ve been asked by so many people about this video over the last few weeks and it’s been killing me to see such misinformation spread around.
By the way, Terry Tao did an excellent (dense, as usual) write-up of the real mathematics behind the “identity.” See http://terrytao.wordpress.com/2010/04/10/the-euler-maclaurin-formula-bernoulli-numbers-the-zeta-function-and-real-variable-analytic-continuation/
LikeLike
That link is great (as, apparently, is everything that he does), but I liked Bryden Cais’s discussion here more: http://math.arizona.edu/~cais/Papers/Expos/div.pdf
Points I felt that his write-up highlighted:
(1) moving terms of an infinite sum around is problematic with a hint why
(2) the Cauchy definition of convergent series necessarily creates a definition of non-convergent series
(3) a core activity of mathematicians is taking a definition extending it (keeping some properties and eliminating others), then seeing what happens
(4) another core activity is finding links with other areas that hadn’t originally seemed connected
Maybe I need to add a disclaimer: Bryden is a friend of mine.
LikeLike
Great link! This is one note I have been reiterating to my friends over and over:
> One cannot hope for the rearrangement of terms in a divergent series to be an innocent operation, as this is already not the case for conditionally convergent series.
LikeLike
Thank you for this. It’s annoying when the explanation is avoided by saying something along the lines of “and now using some very complex reasoning / magic we get what we get”. so very finance at times.
LikeLike
Yeah, I saw this and just dismissed it as obvious bunk. But I’m very glad others chased it down and clarified things with the Slate author who popularized it.
It’s too bad what I am reading still obscures why there is any connection at all between this divergent sum of positive terms and a small negative number, which is very pretty.
The big motivation is that zeta(-1) = -1/12 by usual analytic continuation, and the sum of positive integers is what you get formally when you insert -1 into the usual defining series for zeta.
And I see if you want you can apply summation methods with a smooth cutoff and get expansions for the divergent sum where -1/12 is the leading constant term ahead of a term scaling as N^2 times a positive constant and an O(1/N) remainder. That’s neat, but a stretch for a general math audience. The Terry Tao page discussion is the best here and points to some nice general results.
Hopefully a few people will find some inspiration out of this episode.
LikeLike
@bindicap and mathbabe:
Bindicap says “It’s too bad what I am reading still obscures why there is any connection at all between this divergent sum of positive terms and a small negative number, which is very pretty.”
I am intrigued that this seems not simply to be one in a long line of fallacious proofs (which can prove anything = anything else) but that apparently there IS a “connection at all between this divergent sum of positive terms and a small negative number, which is very pretty’.
Or, as Rondam Ramblings says (before refuting the idea)
http://blog.rongarret.info/2014/01/no-sum-of-all-positive-integers-is-not.html
” (Aside for mathematicians: yes, I am aware that the claim is true under Ramanujan summation. That is not the point.)”
Or, as the video claims, the result is useful to string theorists.
That is, that this is not simply nonsense.
So, I would be very curious to see the explanation of that.
Note: It may be that the best explanation is given here:
and I just need to work through it.
But I would love to know if there is a simpler or intuitive discussion as to why that result actually does make sense in some context at all.
LikeLike
So the video argument was about 3 formal series; S1 = 1 – 1 + 1 -…, S2 = 1 – 2 + 3 – 4 + …, and then S = 1+2+3+4+…
It turns out these formal series correspond to eta(0), eta(-1), and zeta(-1), which equal 1/2, 1/4, and -1/12, respectively, where (Dirichlet) eta and zeta are related classical special functions that have power series converging for Re(s) > 1. In a way, the video identifies the “sum” of these divergent series with the corresponding special function value, but hides that identification and pretends instead to be doing series manipulation that is just bogus. Because the formal series come from functional series that do have a domain of convergence where the math is legit and works, you luck out and the unjustifiable formal series manipulations work out too.
The crux of the legitimate argument is a very nice functional equation that you can easily verify by manipulating the power series for eta and zeta where they converge absolutely, and then the functional relationship must hold everywhere (even where the series don’t converge) through the power and beauty of complex analysis.
zeta(s) – eta(s) = 2 * 2^-s * zeta(s)
This relationship means that eta(-1) = 1/4 implies zeta(-1) = -1/12 and is the final stage of the video argument.
LikeLike
@bindcap: Thank you very much.
LikeLike
I disagree that the video is destructive to the understanding of maths. A 10 minute video is not the place to start teaching about analytic continuation or the Riemann Zeta function (although they do in fact begin to discuss those in an extended discussion of the video on the numberphile website… they also mention in the video that 1 – 1 + 1 – 1 + … = 1/2 is discussed at length in a separate video, so no need to replicate it again). But the result that, despite intuition, it is possible to assign a finite number to a diverging infinite sum in a consistent manner is absolutely fascinating and absolutely worth making a video about, even if you don’t have time to teach advanced mathematics.
Also, the term “hocus pocus” may have been a poor choice of words, but I’m not sure I’m any more thrilled with “crazy-ass things”.
I’ve had more students ask me about this video, and seen more posts about it on facebook than any other math topic I can think of. It’s getting people thinking about math and, brilliantly, QUESTIONING the result. The mere fact that mathematics can be (must be!) questioned is something that most students never learn.Yes, the discussion is extremely oversimplified, but that’s how education works. In my opinion, this video doesn’t risk confusing the intuition about positive and negative numbers, it takes advantage of that intuition to motivate people and make them curious.
And while I agree that the identity is not true in an intuitively plausible sense, why does that diminish its truth? I’ve always thought one of the beautiful things about mathematics is that ‘intuitive’ and ‘plausible’ have nothing to do with ‘truth’. To quote from A Few Good Men: “It doesn’t matter what I believe, it only matters what I can prove!”
ps – I took your Number Theory class at Columbia a while ago, and wanted you know that I really enjoyed it! It was great to have a professor who so obviously loved mathematics, and so obviously cared about sharing that with students.
LikeLike
I think the bigger problem is that they’re misrepresenting mathematics both by their flawed reasoning and by an appeal to authority replacing good logic.
The video on Grandi’s series doesn’t do any better, because they say there that taking averages of the sequence and looking at that limit is how you get 1/2. But they don’t make it clear that this is not the same as a usual sum, or that the two definitions are totally contradictory if you use them interchangeably.
That they have such a huge audience makes it all the more imperative that they do it right.
LikeLike
> … they say there that taking averages of the sequence and looking at that limit is how you get 1/2. But they don’t make it clear that this is not the same as a usual sum, or that the two definitions are totally contradictory if you use them interchangeably.
This is worded so imprecisely that one can interpret it very leniently.
But you do know that Cesàro summation properly extends ordinary series summation?
http://en.wikipedia.org/wiki/Ces%C3%A0ro_summation
Which leads to the question of what you mean by ‘totally contradictory’.
LikeLike
Then let me be more precise: the equality symbol is what’s being overloaded here, and if you switch the meaning of equality you can derive contradictions.
Cesaro sums extends ordinary summation only for absolutely convergent series (conditionally convergent series have useless sums anyway). This is not extending ordinary series summation, because it gives different answers for some (but not all) divergent series. Anyway, “has no sum” and “has a sum” are contradictory if you don’t specify what kinds of sums they are. This is what I mean.
LikeLike
j2kun:
I understand your irritation at seeing some horrible, “careless” piece of math that needs to be junked away super-quick.
But I think you’re letting your dismissiveness spill over into making statements that themselves mislead.
Given the public nature of this blog, I’ve filled in some of the gaps and I ask for your forbearance.
> Cesaro sums extends ordinary summation only for absolutely convergent series …
Cesàro summation applies to all convergent series, whether absolutely or merely conditionally. What that means is that as long as a series converges, both ordinary and Cesàro summation will give the same value [1].
The additional power of Cesàro summation is that it evaluates some divergent series as well, such as Grandi’s 1-1+1-1+….
> … (conditionally convergent series have useless sums anyway).
What could this possibly mean? How is the classic 1 – 1/2 + 1/3 – 1/4 + … = ln 2 useless?
[1] http://math.stackexchange.com/q/207910
LikeLike
Conditionally convergent series fail to retain their “limit” upon a choice of rearrangement of terms. There is a theorem to this effect. If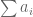 is a conditionally convergent series, then for any real
is a conditionally convergent series, then for any real 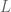 there is a rearrangement of the terms so that the limit of the resulting series is
there is a rearrangement of the terms so that the limit of the resulting series is 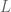 . So to say that a Cesaro sum coincides with a conditionally convergent sum is not very useful. Both can be anything you want them to be just by rearranging terms.
. So to say that a Cesaro sum coincides with a conditionally convergent sum is not very useful. Both can be anything you want them to be just by rearranging terms.
LikeLike
I too think there was a lot of good that came from this tempest in a teacup. Not to mention bringing up some key questions rarely brought to light:
* Should widely popular videos be ‘right’? According to whom?
* How should math be taught?
So much of math teaching is shit-tastically boring. A piece of math, interestingly wrong, can be very effective as part of a solution.
LikeLike
I agree that we often have to make choices when presenting math stuff to a general audience, and often we sacrifice some amount of precision or power or details for the sake of getting a more general idea across. Obviously it’s silly to say “but they should have crammed a course in complex analysis into this video to properly explain analytic continuation and the Riemann zeta function. But I really think the video is misleading. (I have advanced calculus students who told me that this is true but have no idea in what sense it’s true and what is meant by “sum” in this case-but it’s still early in the semester, so I’ll straighten them out.)
I disagree that it would have taken too much time to provide a non-misleading answer. It would have taken under 10 seconds to say, “We can’t find a sum in the usual sense, but we can still assign a value to this series in a way that is meaningful and useful. Don’t try these series manipulations at home.”
Shameless plug: You can read my blathering about this video here: http://blogs.scientificamerican.com/roots-of-unity/2014/01/20/is-the-sum-of-positive-integers-negative/
LikeLike
Cathy, you are exactly right — we mostly agree but there is a mild disagreement between us on a point I think is really interesting! Super busy day but I’ll try to blog about this tonight.
LikeLike
If you’ve still to write your blog note on this topic, I’d be curious to know your take on this:
This video overloads notation about which most non-expert viewers have strong intuition (arithmetic in real numbers) and weak intuition (convergence of infinite series). The presenter plays on that intuition to justify each step instead of giving a more complete explanation.
How do viewers respond:
– some may be inspired to investigate further and find a more complete discussion
– some may feel their intuition for convergent series weakened further, possibly concluding that they don’t actually understand what’s going on and have no remaining intuition.
– some may question their understanding of arithmetic in real numbers
There are certainly many other similar examples in math, but my memory is stronger for cases in my physics classes:
– applying finite dimensional vector space results to infinite dimensional vector spaces in quantum mechanics
– talking about the Dirac delta as a function. Talking about Dirac delta as the derivative of the step function
– Treating e^m the same whether m is a matrix or a complex number
LikeLike
On the one hand, the result could be taken as a reductio, proving the identity is an error. On the other hand, if the result is used in physics, that implies that there’s a difference between a purely mathematical result and the dynamic process averaging the sums. On the third hand, Brouwer would have a fit. Therefore I have three hands.
LikeLike
It’s “jibes with”, not “jives with.”
LikeLike
Thanks, I fixed that!
LikeLike
I am no mathematician, but speaking purely as as one who had difficulty getting a c+ in high school math fifty plus years ago, why can’t that series be re-written as (1-1)+(1-1)+(1-1)…,and why doesn’t that reduce to 0+0+0… ?
And if so it certainly seems “intuitive” to me that the sum of an infinite number of zeros is still zero.
Surely I am missing something trivial and obvious and I hope someone will explain it to me.
LikeLike
You are right, you could in principle argue the sum is zero. What you have done is what is called “rearrange the terms”. You could also rearrange terms of the series as follows: 1 +(-1 +1) + (-1 +1) … = 1+0+0 … =1
and so by using your same technique (rearrange the terms), one could also argue the sum is 1.
If you want to assign only *one* value to a series, then I think the only way out is to conclude that you must disallow your technique of “rearranging terms” as a way of assigning a value to a series. Most mathematicians I suspect are in the camp of wanting to assign only one value, but it is perhaps (I don’t know, this is not my field) an interesting question of what are all possible values a series can be given if you allow rearranging terms. Bryden Cais’s write-up says one can rearrange the series $$1 – 1/2 + 1/3 – 1/4 + ..$$ to obtain any real number as a sum (but I don’t think he gives a proof and I don’t immediately see the proof).
Your way of assigning a value (allowing rearrangement of terms) only gives a unique value for some series (I’m guessing the technical requirement is what is called “absolutely convergent” but I’m not a 100% sure), and 1-1 + 1-1 .. is not one of them.
It turns out mathematicians have developed some techniques (cesaro summability, analytic continuation, possibly others) for assigning a unique value to a larger class of series that includes 1 – 1 +1 .. and if you apply those techniques to this case, you get 1/2.
I learned all this just now by reading Bryden’s excellent write-up
Click to access div.pdf
Thanks Bryden!
LikeLike
You’re absolutely right!
But why rearrange terms?
Laypeople would ordinarily consider Z+E+B+R+A+S+… to be different from A+B+C+D+E+….
And experts *know* the sequence of terms is meaningful.
LikeLike
Part of the problem with the looseness is that someone with an incomplete understanding won’t really know what types of rearrangements are acceptable and which aren’t. For example, shifting a “series” by prefixing with a finite number of 0 summands doesn’t change whether or what they converge to (in both Cauchy convergence and Cesaro convergence), but someone might think that is an illegal rearrangement. Or, more likely, they will worry that it is illegal, but not know and not really know how to check.
LikeLike
I’ve explained 0.9999. . . a few times to people, and why it’s understood to mean a limit, and so it really is 1.
LikeLike
I don’t know how to make videos, but I tried to give my take on some of the “crazy ass stuff” (for non experts) in my blog (http://samenamemath.wordpress.com/). I really should figure out how to make good math videos…
LikeLike
People seem to like Tao’s post, but disregard his linked blogpost entitled “There’s more to mathematics than rigour and proof”. As mathematicians we offer/tease people with paradoxes all the time. This is a good thing, not a bad thing.
LikeLike
Personally I hate the idea of a “paradox.” Whenever I hear someone say paradox it means they don’t understand something. They should just say “I’m confused.”
LikeLike
How about “paradox” as shorthand for “apparent but not actual contradiction” ?
LikeLike
That would be better but only if you actually dig around until you understand why it’s _not_ a contradiction. The danger with “paradox” is that people leave it at that.
LikeLike
Absolutely. The point of a paradox is to expose something deeper — which only happens when you investigate and understand it. Are you not a fan of the Banach-Tarski Paradox? There are many such things and many lead to deep(er) math. Analytic continuation is an excellent example of that.
re: people leaving it at that : I don’t think the problem is with the word paradox, but a wider issue in math education/popularization. But I take your point about miseducating people to think that mathematics contradicts itself.
LikeLike
Also — thanks again for a thought-provoking read.
LikeLike