When is math like a microwave?
When I worked as a research mathematician, I was always flabbergasted by the speed at which other people would seem to absorb mathematical theory. I had then, and pretty much have now, this inability to believe anything that I can’t prove from first principles, or at least from stuff I already feel completely comfortable with. For me, it’s essentially mathematically unethical to use a result I can’t prove or at least understand locally.
I only recently realized that not everyone feels this way. Duh. People often just assemble accepted facts about a field quickly just to explore the landscape and get the feel for something – it makes complete sense to me now that one can do this and it doesn’t seem at all weird. And it explains what I saw happening in grad school really well too.
Most people just use stuff they “know to be true,” without having themselves gone through the proof. After all, things like Deligne’s work on Weil Conjectures or Gabber’s recent work on finiteness of etale cohomology for pseudo-excellent schemes are really fucking hard, and it’s much more efficient to take their results and use them than it is to go through all the details personally.
After all, I use a microwave every day without knowing how it works, right?
I’m not sure I know where I got the feeling that this was an ethical issue. Probably it happened without intentional thought, when I was learning what a proof is in math camp, and I’d perhaps state a result and someone would say, how do you know that? and I’d feel like an asshole unless I could prove it on the spot.
Anyway, enough about me and my confused definition of mathematical ethics – what I now realize is that, as mathematics is developed more and more, it will become increasingly difficult for a graduate student to learn enough and then prove an original result without taking things on faith more and more. The amount of mathematical development in the past 50 years is just frighteningly enormous, especially in certain fields, and it’s just crazy to imagine someone learning all this stuff in 2 or 3 years before working on a thesis problem.
What I’m saying, in other words, is that my ethical standards are almost provably unworkable in modern mathematical research. Which is not to say that, over time, a person in a given field shouldn’t eventually work out all the details to all the things they’re relying on, but it can’t be linear like I forced myself to work.
And there’s a risk, too: namely, that as people start getting used to assuming hard things work, fewer mistakes will be discovered. It’s a slippery slope.



Cathy, I can’t tell you how much what you say resonates with me.
LikeLike
Thanks!
LikeLike
In my view, much published research in finance does something worse. It doesn’t define its terms. It enters into debate in a putatively precise manner about some concept, such as, say, “fair value” without making an adequate effort to define it, then sets about writing mathematical formulas about things it hasn’t defined. This, I suppose, must be how those debates about how many angels could stand on the head of a pin must have occurred.
LikeLike
Cathy, I remember when I had the same realization while I was a graduate student. I ended up choosing, unconsciously, a dissertation project that was low-enough level for me to be able to prove pretty much every result I used. I even found an error in a paper that I ended up using. (I found a second error in the same paper five years later — fortunately not in a result that I used in my dissertation!) Like-minded people can find similar work by avoiding certain advisors and fields and being conscious of their choices and their consequences. For instance, such work might not be likely to land one a job at an R1 school (but as you have said, that should not be the presumptive goal of graduate school anyway.)
Your post made me realize that while, as you have said, proof is a social construct, it is separately a personal construct. Through time we can lose the ability to construct truths that we formerly could, and I would think it is easier to trick yourself into belief than it is to trick society. But perhaps not — is there a “research bubble” rolling down that slippery slope?
LikeLike
I like that – the personal construct is sometimes not in line with the social construct. And of course different people disagree on what the social construct is anyway.
LikeLike
At my school the unofficial position was that all four-year degrees were in fact five-year degrees. Old-school guys, of course, who came up some time in the 70’s or 80’s. Plus a few insane types who wanted the rigor _and_ demanded that you do it in four years. After all, that’s what they did 😉
LikeLike
I think “be able to prove on the spot” is too high a bar, and any mathematician who makes us (especially math students!) feel bad about inability to “prove on the spot” is a jerk and a hypocrite (I say this, of course, with full knowledge that I regularly ask my students to “prove on the spot” during in-class exams). I doubt that I can “prove on the spot” some of my own published proofs, and I certainly cannot “prove on the spot” an involved theorem, such as Grothendieck-Riemann-Roch, that is, nonetheless, used on a regular basis by a large number of algebraic geometers.
However, I do understand the strategy of that proof at a high level, I understand many of the details very well, and, *when necessary*, I “can” read through and verify the remaining details. I believe this is the “industry standard” in mathematics. We should be able to verify proofs “when necessary”, and we should try to be scrupulous with ourselves about when it is “necessary” to go through proofs.
That does not address the main issues: should we believe a proof that we have not yet thought about deeply ourselves, and is the community sufficiently diligent in preventing mistakes from entering the “canon” (which I think of as separate from “the literature”, especially in these days of proliferating journals). That is certainly not a new problem, cf. the battle between Riemann and Weierstrass. However, I do not believe that attitudes have become more lax in modern times; I expect we are far more strict about rigor than our predecessors working one hundred years ago. I do believe we are less hypocritical; no longer does every mathematician pretend to be an expert on every result, nor does every referee pretend to have verified every detail. We, rightly, identify correctness as primarily the job of the author. In the wider view, verifying correctness is the job of the community as a whole. Any single referee is liable to miss a detail. Only results that stand the “test of time” after careful review by many readers are accepted as “canon”.
LikeLike
Cathy,
Fantastic post. I had almost exactly the same experience as you and have not seen this discussed before. For me, it all starts with the feeling of satisfaction and finality I get from “owning” a proof. To me that means being easily able to conceive how I would have thought of it myself from beginning to end, if only I had been clever and lucky enough. If a proof is based on results I didn’t own, then I can’t own it. I just don’t get satisfaction from things taken on faith, even if it is faith in very smart and careful people whom I know I should trust. Those who feel this way, I suppose, will necessarily feel that those who act as if they own a result, when they don’t meet our internal standards for ownership, are behaving “unethically,” or at least with a somewhat unjustified pride — much as there is a spectrum of standards for what constitutes “earning” money.
Of course, there is a practical side: if you own a proof, it will be much easier to know which variants on the result are true. If I really knew how a microwave worked, presumably I would know not to stick something metal in it without being told.
LikeLike
A friend of mine agreed to pursue his math Ph.D. about 30 years ago only on the condition that his dissertation be understandable to most any mathematician. He studied convex lattice polytopes.
LikeLike
this is my problem! and i had a very poor background to begin with so yeah. but i think i have a further problem which i can’t tell if you also had, which is that i think it is much harder for me to Feel like i “understand” something. it’s not that i am opposed to using something i can’t make myself; it’s more that if you don’t tell me How to use a microwave, you just say “put this particular plate of food in, press these four buttons in this particular order” i will have no idea how to microwave anything else. i think other people are very comfortable saying hmm maybe i can put this other food in the microwave, let’s see! maybe i can put any container in the microwave, let’s find out! i wonder what this button does! but i don’t feel that way because, to keep with the analogies, i could put a plastic bowl full of soup in the microwave and never realize via personal experimentation there’s chemicals leaching into my food. i could set the timer too high and burn myself when a surprise bubble pops up as i try to get the bowl out (i think that happens?). with math, it’s not like if i misunderstand something my paper will beep at me until i correct it. so it makes me really uncomfortable when someone explains something to me and i know in my heart that if s/he negated a couple sentences (thus rendering everything false) i would not be able to tell it was wrong at all. and it doesn’t help that i’ve had the experience many times over where someone explains something to me and it makes sense and then later they so oh no that was completely wrong.
LikeLike
Yes I definitely experience exactly that kind of anxiety when using something I don’t understand completely.
LikeLike
This problem certainly isn’t limited to mathematicians! I’m a biologist and I constantly wrestle with this problem and it negatively affects my productivity. I am trying to be cautious and careful to ensure that the assertions I make are as correct as I can reasonably make them. Towards that end, I’m never sure how many levels back I should go in reading the references of the papers that I cite. What if one of the key assumptions in the paper that I’m citing was wrong, thereby invalidating the legitimacy of the paper I wish to refer to, and then perhaps my own? I am concerned with maximizing my signal to noise ratio even if that comes at a cost of producing fewer signals. A lot of that stems from my own anxiety and insecurities though. I never feel as though I’m good enough for the field that I’m in. I don’t feel like I’m smart enough or that I belong here. I feel like I’m just waiting for the shoe to drop and all my colleagues to realize I’m an idiot. So that worry and concern drives me forward to be ever more careful, all the while this anxiety greatly hinders my productivity. Although the irony of this is that it also allows me to produce nearly nothing (or a small fraction of what I could produce otherwise) comfortable in the knowledge that at least I haven’t created any disinformation.
Ultimately that’s more about me and my confidence than anything else and it entails a great deal of hubris. My singular works and thoughts are ultimately that important, and myself (and potentially science) also suffers an opportunity cost in attempting to obtain a level of perfection that doesn’t exist. I am like a virtual Sisyphus, except instead of being forced to push a rock up a hill repeatedly only to have it roll back down again, I am forever trying to get a little bit further up on the asymptotic plateau of ‘good enough’. I lack the world view and experience to know when the landscape is flat enough.
One of the great things about science is that even if we get something wrong today, in a decade or two some super keen graduate student is going to come along and re-question everything- check that we haven’t made any critical mistakes and point them out when they are ultimately found. Further towards that end, even if the field of mathematics (and everything else) becomes substantially larger and more complicated, the number of people achieving advanced degrees will also grow- so while the distribution of knowledge across sub-disciplines within a field narrows with increasing discoveries, so do the number of it’s practitioners. Hopefully that will ultimately balance out.
Love your blog,
Brad
LikeLike
That is a familiar feeling to me. I’m only a little undergrad, but I feel I have come a long way in conquering the feeling by being candid about such feelings, and by reading/listening to those who have achieved results that I think important. To know that thinkers I admire like Bertrand Russell and Andrew Wiles too had their moments of doubt is very reassuring.
Also this feeling is what has prompts me to a very frank evaluation of the past 200 or so years of mathematical and philosophical thought (a journey I am in the midst of), and examining the foundations (what MUST be true or we don’t exist) gives me confidence at least that my foot is on ground *somewhere* down there in the mist.
I can’t vouch for your abilities personally since I know nothing more than what you’ve divulged here. Yet I feel certain that your colleagues will not “find you out,” because there is probably nothing to find out. Finding out the truths of Nature is not easy, and humans are only humble, fragile creatures who only (relatively) recently figured out that there is material in life that encodes protein synthesis. We do our best. We try one idea, and if that one bears no fruit, we go back and try a different way. That is the story we write, and as long as we have passion and means to learn of Nature’s structure, we are good enough to help each other find light in the darkness. I feel this goes for mathematics, biology, and all other sciences.
LikeLike
Okay, I am about to make a comment that will probably go over badly. So let me start by saying that I am likely misinterpreting some of what has been said. And, at any rate, this whole issue is one of the most charged in mathematics and easily leads to strong disagreements. Nonetheless, here is my (probably incorrect) observation: some of what is being said here sounds, at least a little bit, like humblebragging: “I guess there is something wrong with me because I personally cannot bring myself down to the slipshod, basically unethical, and (perhaps) intentionally deceitful practice of many professional mathematicians today.” If you honestly feel that the profession today is shot through with bad practice, I invite you to read a few articles from one hundred years ago. Read Euler! The standards are extremely high today.
The “industry standard” is not to write proofs in research articles with every i dotted and every t crossed; research articles are not intended to be easily read by undergraduates or even all PhDs. Of course the literature is not presented that way simply to cause confusion or exclude the “non-select”. Articles, and lectures, are presented the way that they are because it would be absolutely unworkable to spell out every detail. If you think that is a lame excuse, read about the Herculean efforts of people in the automatic theorem proving community simply to code basic theorems of single variable calculus. It is insane to expect mathematicians to include all details. It is insane to demand students to check all details. It is essential that students be able to check all details that are “necessary” and to recognize when those “necessary” occasions arise.
That does not mean that it is wrong to question the standards of exposition, the process by which the community assigns credit, acknowledges and correct mistakes, etc. Once again, all of the above is quite likely due to a misinterpretation on my part, and I apologize if I got it wrong.
LikeLike
I agree that the standards are admirably high today in contrast to the time of Euler. And while I agree that it’s unworkable to check every detail of every argument, your argument would apply equally well to allow every paper to degenerate into a sketchy mess. It needs to be workable to demand either details or references – else what are we doing?
LikeLike
That said I strongly appreciate your use of the term “humblebrag” here.
LikeLike
re humblebragging, growing up i had trouble doing in class writings because i couldn’t get anything down on paper. i was thinking; i wasn’t blowing it off, but i couldn’t write anything down. at some point i was told it was my “perfectionism” getting in the way. that i needed it to be “right” before i wrote it down. i think this was a fairly objective assessment of the situation, but i could have told anyone loudly and arrogantly that “My only failing is realizing that with my superior intellect, perfection is within my grasp and thus I cannot stand to lower my standards merely to turn in a completed assignment on time. My integrity is worth far more than my grade!” but my problem was nothing to brag about even if it contained the word “perfect.” i haven’t read all of the comments carefully but i just want to say that it is not inherently arrogant to have the complaints mentioned above even though an arrogant person could certainly spin it that way.
LikeLike
Jason’s points about proofs are insightful, but r.e. humblebragging: I think a defining characteristic of “humblebrag” is that the surface message of the statement is one the author doesn’t care in the slightest about and would never bring up on its own– it is solely an excuse to slip in the brag. That doesn’t look like the case to me at all here — the post starts an interesting conversation about how people think about proofs, and whether it makes the author look good or bad is incidental. There is no mandate to actively *avoid* topics that might reflect well on you! (or that others might think you think reflect well on you 🙂 )
LikeLike
In my field, linguistics, syntax shows a parallel growth: it’s become a little cottage industry but it seems that ever fewer practitioners have a grounding in its mathematical proof-theoretical origins of automata and cryptography. As syntactic speculations grow more complex, those outside the field are left increasingly disgruntled and skeptical, sort of like angry Occupy Wall Streeters’ protesting financial complexity that the bankers themselves no longer understand.
Back in the ’80’s generative semantics had a huge intellectual bubble and actually did collapse. Chomsky pulled the plug on it, like Paul Volcker raising interest rates to stem inflation. Didn’t curtail the growth of syntax, though. Neither those who practice it nor those who criticise it have Chomsky’s mathematical background or interest. Syntacticians continue to construct daunting sand castles while critics scoff. No one can see the foundation, so rejecting it is as much an article of faith as playing in it.
LikeLike
What would you think if people used results whose proofs were verified by computer without necessarily understanding the proofs themselves? That way one could at least be confident of correctness.
LikeLike
That’s the advantage *and* disadvantage of computational linguistics. Easy to tell if a model works even without thinking, harder to tell whether it says anything about human language.
I wonder if there’s any available analogy to the dismal science.
LikeLike
Correction in my post: “automatic theorem proving” –> “interactive theorem proving” (systems such as Coq).
LikeLike
I had a related problem in my chosen field of computer science. One major goal of the discipline is to allow people to choose their best level of working abstraction and not have to worry about the underlying details like the language implementation, the operating system or the hardware. So, I would blithely start one project or another with a chosen set of tools at a desired level of abstraction and all too quickly run into quicksand and find myself pulled down into deeper and deeper levels of distrust, mistrust and paranoia. Nothing was ever quite as it appeared on the surface, and the deeper one was pulled, the more apparently unrelated issues moved to the front and center. Compiler problems would be traced to memory hardware interactions with the input output system. Library problems would be traced to memory allocation problems or faulty numerical analysis and error handling in exotic substrata. It was like going in to watch some Disney fluff and finding oneself in a film noir.
At first, I resented having to learn so much more than I intended and wishing that I really didn’t have to know quite so much to get the job done. Then I learned to sit back and enjoy the ride on the crazy roller coaster knowing that at some point I could bend and twist teh track and ride it home.
In mathematics, it seems you can choose to accept riding on the surface or taking the deep dive. In computer science, you have to accept the ride.
LikeLike
Quote: The amount of mathematical development in the past 50 years is just frighteningly enormous, especially in certain fields, and it’s just crazy to imagine someone learning all this stuff in 2 or 3 years before working on a thesis problem.
LikeLike
Quote: The amount of mathematical development in the past 50 years is just frighteningly enormous, especially in certain fields, and it’s just crazy to imagine someone learning all this stuff in 2 or 3 years before working on a thesis problem.
Yes, but it’s less frightening if you don’t believe in the myth of mathematical “progress”. It is certainly legitimate to go back in mathematical time and look at paths not taken. And we always have total freedom to re-examine foundations.
P.S. Sorry for the abortive post #22. I’m new at this.
LikeLike
First, I love this post, and thanks for sharing your honest thought.
I think I am trying to resolve the same “problem” by thinking mathematics as understanding [if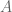 is true, then
is true, then 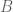 is true], instead of understanding [
is true], instead of understanding [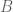 is true]. This way, I do not feel unethical, and the work to bridge some fact (or axiom)
is true]. This way, I do not feel unethical, and the work to bridge some fact (or axiom) 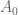 to
to 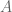 still remains, but I don’t need to do “boring” homework right away.
still remains, but I don’t need to do “boring” homework right away.
I am still far from being a professional mathematician, but so far this works for me.
LikeLike
I think your way of looking at math is the way one should look at it. I also think that all the really good mathematicians refuse to use machines they don’t understand, and demand that they understand those they do use. Moreover, the very best mathematicians, a Gromov or Thurston, for example, are notable for how they reexamine the basic things a lot of folks unreflectingly take as clear or obvious. To continue the example, with Gromov and Thurston I am always struck by how much of the work of both can be understood as an elaboration of the geometric content of the first course in complex analysis. To put an example closer to home, look at Bhargava’s most recent preprint with Wei Ho (which attributes certain results to one Cathy O’Neil). Someone’s been thinking hard about something so trivial as three tensors … and prehomogeneous group actions.
LikeLike
There is something to be said for your idea that you should understand all the mathematics you use.
I heard a mathematical horror story once (no idea whether it was true). This graduate student was given a paper by his advisor and told “see what the results in this imply. He started working out really interesting consequences of this result, until finally he proved one theorem that his advisor knew to be false. Eventually, he and his advisor discovered the bug in the original paper. But he had wasted over a year of time on work that was unpublishable.
LikeLike
Yuck!!
LikeLike
I like to really understand the proofs of all the results I use in my work. But often the quickest way for me to reach this point is to start by reading lots of definitions and theorems and example while skipping most of the proofs. Instead, I focus on how things work in examples, and how they fail to work in counterexamples. For each theorem, I mentally go through a few examples and see how it goes. Once I get “the lay of the land”, I’m ready to read the proofs. A lot of them will be pretty obvious at this point. Then I can put most of my energy into the hard ones.
When I was younger, I would waste a lot of time reading math books in a more linear way, trying to understand each proof in detail before moving on to the next.
LikeLike
Watch out for using the word “microwave”. There’s actually microwaves in physics, and they have equations and numbers related to them
LikeLike